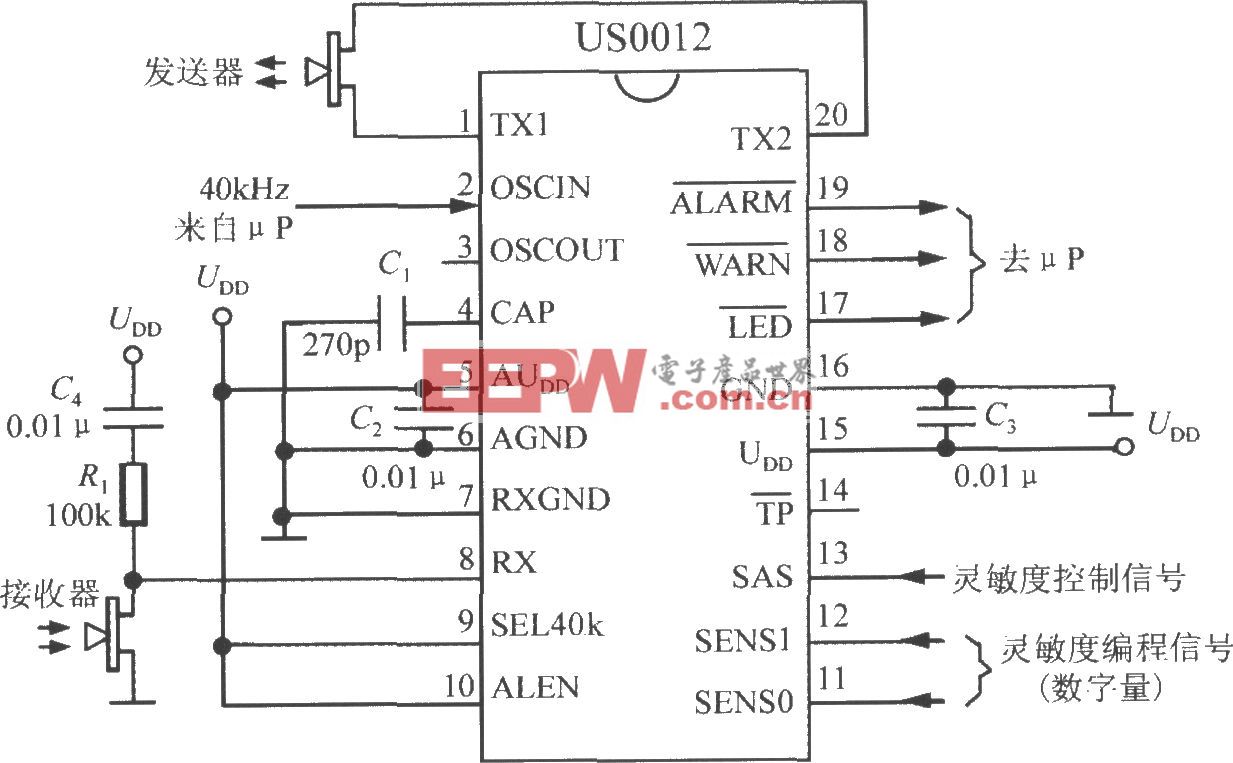
「技术文章」使用有效位数(ENOB)对ADC建模
了解ADC的ENOB(有效位数)的概念,以及如何将其用于系统仿真中的数据转换器建模。
在本系列关于数据转换器建模的上一篇文章中,我们讨论了ADC模型提出了如何选择一个输入信号来实现一个模型。(请注意,这篇初始文章包括一个重要的缩略语、词汇表和参考文献。)
在这里,我们将继续讨论这个话题,讨论数据转换器常用的一个优点,即“有效位数”或ENOB([4]到[8])。
ENOB被定义为一个理想量化器在相同条件下必须执行与数据转换器相同的比特数。可以使用图1中显示的模型,其中NE= ENOB.
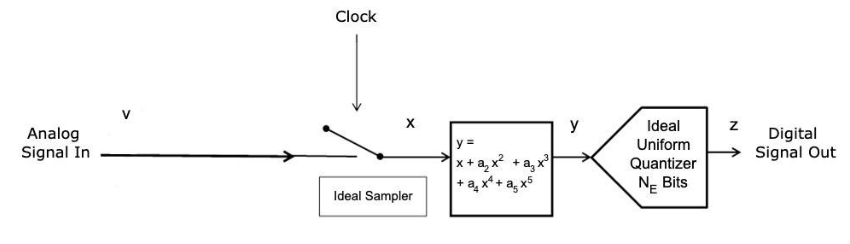
图1ADC模型
问题出现了:“这些条件是什么?它们对应用程序的使用是否相同?ENOB是否有不同的定义,应用于不同的应用?
通常ENOB定义为给定频率的0 dBpeakFS正弦波输入[8]。它通常是频率的函数。设LSB电压为L,理想的ADC有N位。
回到图2,正弦波的峰值在FS处+= L((2N/2)-1) and FS- = −L(2N/2).
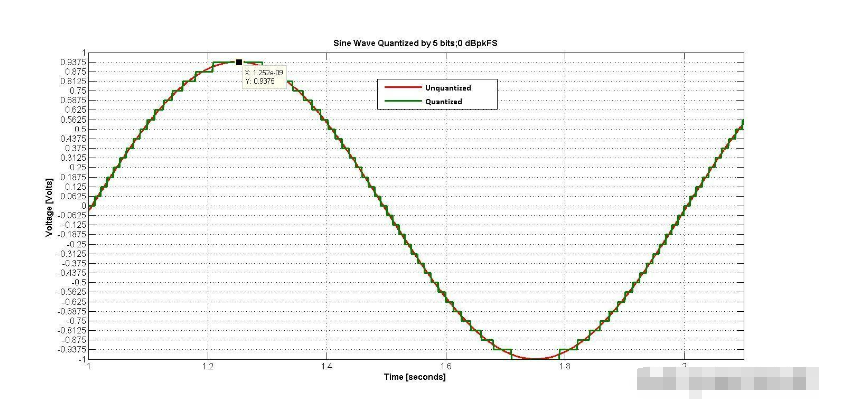
图2上一篇文章中的图2应如何为系统仿真建模数据转换器
对于N≥5;假设L((2)的误差N/2)-1) = L(2N/2) 不到7%,所以我们开始吧。如果正弦波的峰值是L(2N/2) 其均方(ms)值为L2(22号/8). 众所周知,对于理想ADC的随机输入,均方(ms)量化噪声=l2/12([2],方程1.14);这是整个奈奎斯特区的噪声(0到F奈奎斯特). 但是我们有一个正弦波,不是随机输入。您的作者想知道,对于正弦波以及ADC可能看到的其他输入,相同的量化噪声是否有效,所以做了一些简单的模拟。
结果见表1
表1。差分波形量化误差均方进入量化器,无时间采样
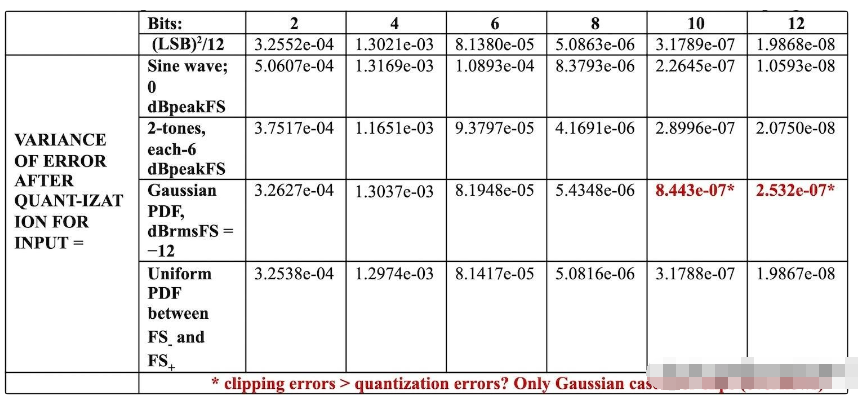
对于2到12位,使用公式L2/12显示均方噪声;并将其与在各种输入下观察到的均方噪声进行比较。即使是单个正弦波,结果也相当接近。唯一的不一致之处是高斯输入,在-12 dBrmsFS,对于10和12位;其中由于单独量化而产生的噪声将很低。然而,高斯噪声的峰值会导致削波(过载),从而增加噪声。
{作为一个有趣的,除了在本文件的.02版中添加的内容外,由Grey[18A]导出了0 dBpeakFS正弦输入下的量化噪声均方值的精确表达式:
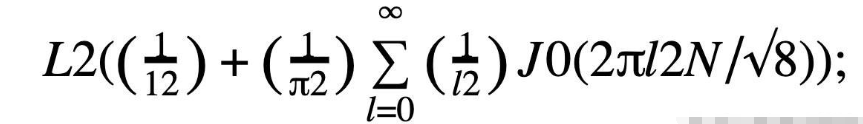
其中J0是0阶的普通贝塞尔函数。对于大x,J0(x) →0;它是L2/12.}
所以,信噪比
SNR=ms(信号)/ms(噪声)=(1.5)(22N)
或者,单位:dB
SNRdB= 6.0206N + 1.7609
方程式1对一个由取样器和一个理想的N位量化器组成的ADC进行了模拟,结果如表2所示。输入正弦与ADC时钟不同步。结果与方程1非常接近。
表2。由方程1和通过模拟ADC正弦波计算的信噪比
对于实际的ADC,整个奈奎斯特区的信噪比和失真比(SINAD)被替换为等式1中的SNR,结果被解为N,现在称为有效位数=NE。
NE= (SINADdB- 1.7609)/ 6.0206 ≈ (SINADdB- 1.76)/ 6.02
方程式2包括非线性失真在内的所有项。对于小于满标度的输入,ADC的失真减小。制造商通常会在某些输入电平上测量SINAD–B dBpeakFS(峰值信号低于满标度B dB)。由于测试输入信号降低了B dB,因此他们会将该值相加以计算ENOB,就好像对于较大的输入而言失真不会增加一样。
NE= (B + SINADdB- 1.76)/ 6.02
伪方程然而,这个公式是假的,因为它忽略了失真会增加的事实,通常比信号快。对于简单的三阶非线性,信号每增加1db,失真度增加3db,因此SINAD将恶化2db。
因为互调是如此的重要,并遵循我们的“选择一个输入信号来实现一个模型”一节的建议上一篇文章:应使用2音输入信号。
还需要探索“测量整个奈奎斯特带宽”和“测量噪声”之间的差异。图3显示了2音测试信号。
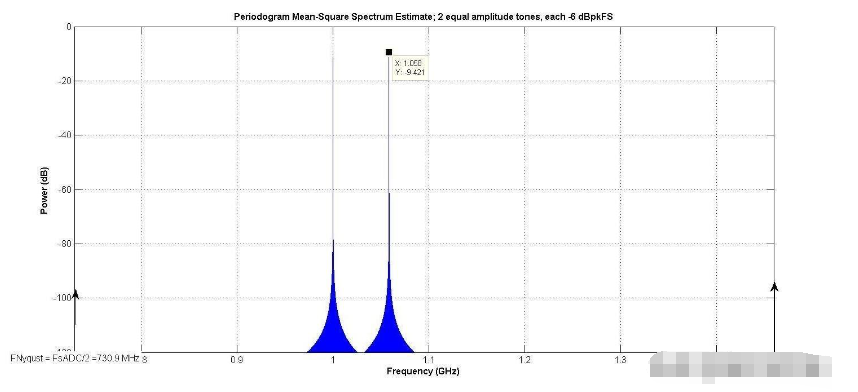
图3
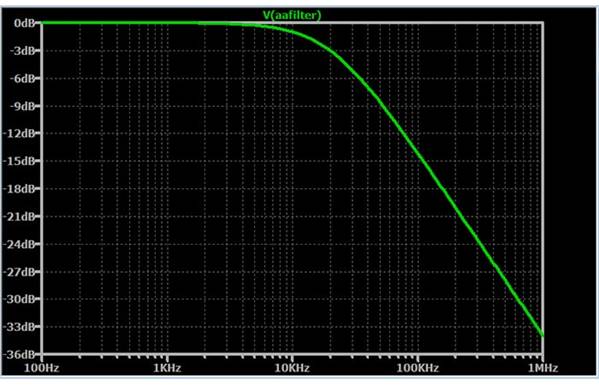
从f开始S= 1461.8 MHz, f奈奎斯特= 730.90 MHz. 信号在第二奈奎斯特区。注意,ADC的输入可以分为奈奎斯特区。由于ADC输出是时间采样的,因此第一奈奎斯特区以上的频率不存在,所以这就是奈奎斯特区。
还使用了1000兆赫的1阶测试信号。“有趣的音调”的中心频率是233.7兆赫。对图1的模型进行了模拟E是理想量化器的位数
图4显示了2音调测试的输出,模拟了一个8位ADC。由于没有明显的杂音(杂散),因此1音和2音输入情况下的SINAD等于SNR。
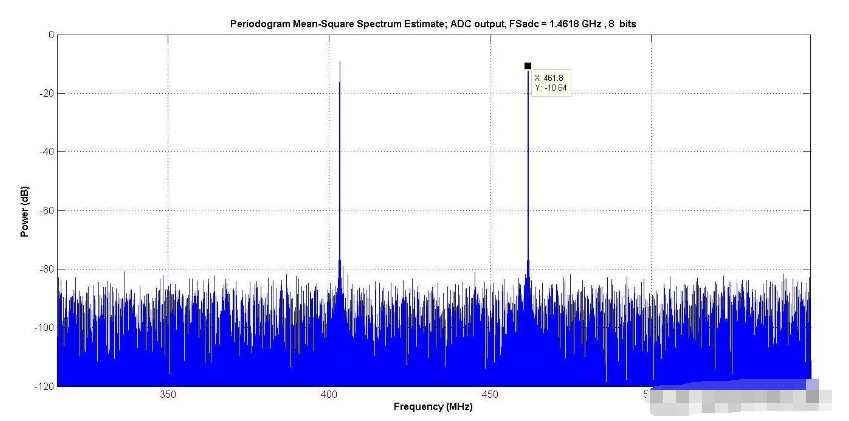
图4
当我们绘制由位函数确定的SINAD时,有两个观测值。
首先,奈奎斯特带宽和“感兴趣带宽”之间的差异是3.1275;相当于4.95 dB。因为这近似于奈奎斯特带宽曲线与相同输入的“感兴趣带宽”曲线之间的差异;这与量化噪声频谱为白色的假设一致。
其次,为了使峰值达到0 dBpeakFS,双阶情况的平均功率必须是单阶情况的½。相同带宽的1阶和2阶曲线之间的差值约为3 dB。
对于单阶输入,它也与等式2很好地匹配。可以定义两个不同的ENOB,将测量的SINAD与ENOB1和ENOB2输入
ENOB1≡ (SINADN1- 1.76)/6.02
式3(a)ENOB2≡ (SINADN2+1.25)/6.02
式3(b)SINADNi是测量的SINAD,单位为dB,用于整个奈奎斯特带宽,用于输入阶。对于图1的模型,两个ENOB是相等的。
本系列的下一篇文章将讨论另一个模型,它使用互调多项式和有效比特数。
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。