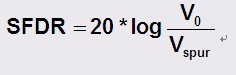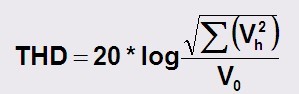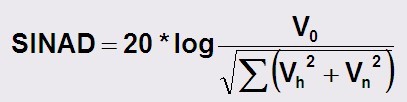如同 Bode 图是理解运算放大器 (op amp) AC 参数的基础一样，傅里叶序列图是理解转换器 AC 参数的基础。在这两种情况下，幅度和相位与时间数据的关系就变为了幅度和相位与频率显示的关系。因为必须要实现从模拟域到数字域的转换，因此对于转换器来说这种转换更为复杂。而信号的傅里叶序列表现是用数学术语来进行充分描述的，无法在标准测试设备上实现。因此，它不如 Bode 图看起来直观。

 

当函数关系可以用一个数学表达式来描述时，时域中信号的标准傅里叶序列就可以被明确定义出来了。但如果该函数仅为 ADC 的数字输出时，那么就需要快速傅里叶变换 (FFT) 了。该变换最早发表于 1965 年，被称为 Cooley-Tukey 算法，并被编写成为很多种计算机程序，此处的重要性在于结果。这就得到了信号带宽中每个频率的幅度。从这个结果中，您可以计算出若干个性能参数。

 

图 1 给出了带有典型 FFT 结果的图。该图是从 ADS8325 产品说明书上复制下来的，ADS8325是一款 16 位 250k 采样速率的转换器。当输入为 10kHz 频率的满量程正弦波时，FFT 显示出了在整个 40kHz 范围内应用信号的每个整数倍频率时的峰值。

 

 

 

 

通过观察可以看出，在这个例子中，无杂散动态范围 (SFDR) 大约为 75dB，应用信号在 10kHz 时为 0dB，三次谐波在 30kHz 时约为 -75dB。这是最大的寄生信号，SFDR 为两个幅度之间的差值。因为确定 ADC 输出的频率是不可能的，因此任何低于 -75dB 的信号都必须被看成是噪声，并且被忽略掉。

 

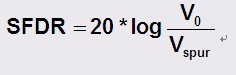
这个公式也可被看成是 dBc，其中 dB 参考电平为载波信号或 V₀。

 

题目为《信号链基础知识：模拟与数字世界》的本系列文章的第三篇文章（2007 年 11 月 30 日发表）描述了与理想转换器相关的量子化噪声。信噪比 (SNR) 的计算为：

 

其中，N 等于比特数

 

因为没有转换器就不会有噪声，所以用 FFT 表示的实际信噪比如下：

 

请注意，该关系式的成立是做了这样的假设：即各种噪声源为独立的，因此，是按照平方值合计的平方根来计算的，或者说是 RSS。

 

任何电路都会有某种形式的非线性，这种非线性特性将在应用信号谐波（整数倍数）时产生信号。

   

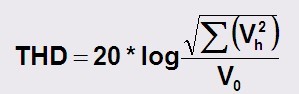
其中：V_h 为 FFT 中谐波电压峰值的列表

 

因为谐波会无限延伸下去，因此必须要有一个合理的谐波次数范围。这里有几个标准，其中之一是IEEE 标准1241推荐用到 9 次谐波。要使总谐波失真 (THD) 值有意义，就必须给出一个谐波次数。

 

由 FFT 演变而来的最后一个描述性术语是 SINAD，或称为信噪失真比。

      

 

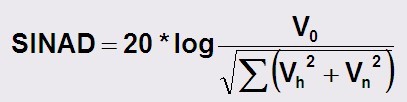
在这些参数中，每一个参数取值的重要性取决于不同的应用。虽然在非线性和失真之间还存在一些相关性，但是这种相关性非常弱。