了解磁芯中的磁场能量和磁滞损耗

在这篇文章中，我们使用磁场能量的概念来探索铁芯磁滞损耗与其B-H曲线之间的关系。

磁芯是许多电气和机电设备的重要组成部分，包括变压器、电感器、电机和发电机。然而，这些核心的一些能量输入不可避免地以热量的形式消散，降低了设备的效率和性能。这些损失产生的热量也会损坏芯材。

我们需要注意的主要核心损耗之一，特别是在高频下，是磁滞损耗。这被定义为由于材料的磁畴与外部施加的场的旋转和对齐而在材料中耗散的能量。

正如你在大学课程中可能记得的那样，磁芯的磁滞损耗与磁芯材料的B-H曲线面积成正比。本文旨在阐明这一基本关系。为此，我们首先需要对电感器如何与电路交换能量以及能量如何存储在磁场中有一个扎实的理解。

磁场能量：概述

电场和磁场都能储存能量。电场中的能量储存概念对大多数电子设备来说都是相当直观的。然而，磁场能量的概念则不那么重要。

考虑电容器的充电过程，它在极板之间产生电场。在电容器的极板上积累电荷需要能量，这是有道理的。随着电容器极板上积累更多的电荷，极板之间的电势差也会增加。如果我们在极板之间创建导电路径，电容器会通过在电路中产生放电电流来释放储存的能量。

现在考虑一个电感器。当电感器携带电流时，它会在磁场中储存能量。建立或增加电流需要一个能源——比如电池——来做一些工作。

为了更好地理解这一点，我们可以看看法拉第感应定律和伦茨定律。法拉第定律告诉我们，增加电感器电流将在电感器的端子之间感应电动势（EMF）。如图1所示，Lenz定律告诉我们，EMF的极性将反对电流的变化。

通过螺线管的电流（a）和EMF对该螺线管的影响（b）。

图1。（a） 沿所示方向的固定电流产生指向左侧的磁场。（b） 当电流增加时，会感应出一个EMF，试图阻止电流的变化。

为了增加电感器电流，进而增加磁场中储存的能量，电池必须对抗感应的EMF。这类似于当我们试图在电容器极板上积累相同极性的电荷时所面临的反对。在这两种情况下，能源都必须做一些工作，并向其负载输送能量。

计算磁场能量

通过使用一般瞬时功率方程，可以找到输送到电感为L的电感器的能量：

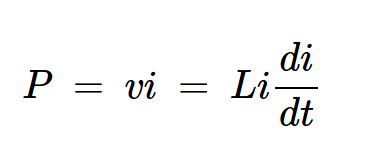
方程式1。

其中v和i分别是电感器的瞬时电压和电流。

在无穷小时间（dt）内提供给电感器的增量能量（dU）为 dU = P × dt

如果我们代入方程式1中的P值，我们得到：

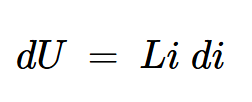
方程式2。

让我们假设电感器的电流从I1变为I2，其中I1和I2都是正值。通过对上述方程进行积分，我们可以得到传递到电感器（U）的能量，如下所示：

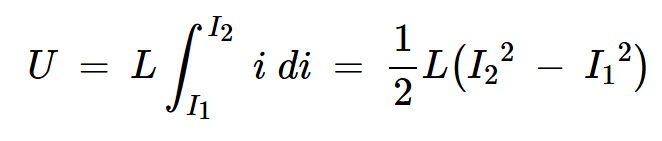
方程式3。

上述方程式显示了电感器中如何进行能量存储。有三种不同的情况需要考虑：

如果电感器电流从I1增加到I2（I2>I1），则U为正。因此，电池向电感器输送一些能量。

如果电感器电流恒定（I1=I2），则U等于零。电感器没有能量输入。

如果电感器电流从I1减小到I2（I2<I1），则U为负值，这意味着电感器充当向外部电路提供一些能量的源。

因此，通过将I2=I和I1=0代入方程3，可以找到具有电流I的电感器中存储的能量。这导致：

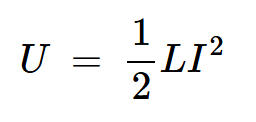
方程式4。

电感器中的能量发生了什么变化？

电感器中存储的能量可以传递到电路中的其他组件，如电容器或电阻器。例如，考虑图2中的电路。

展示电感器如何释放其初始能量的理论电路。

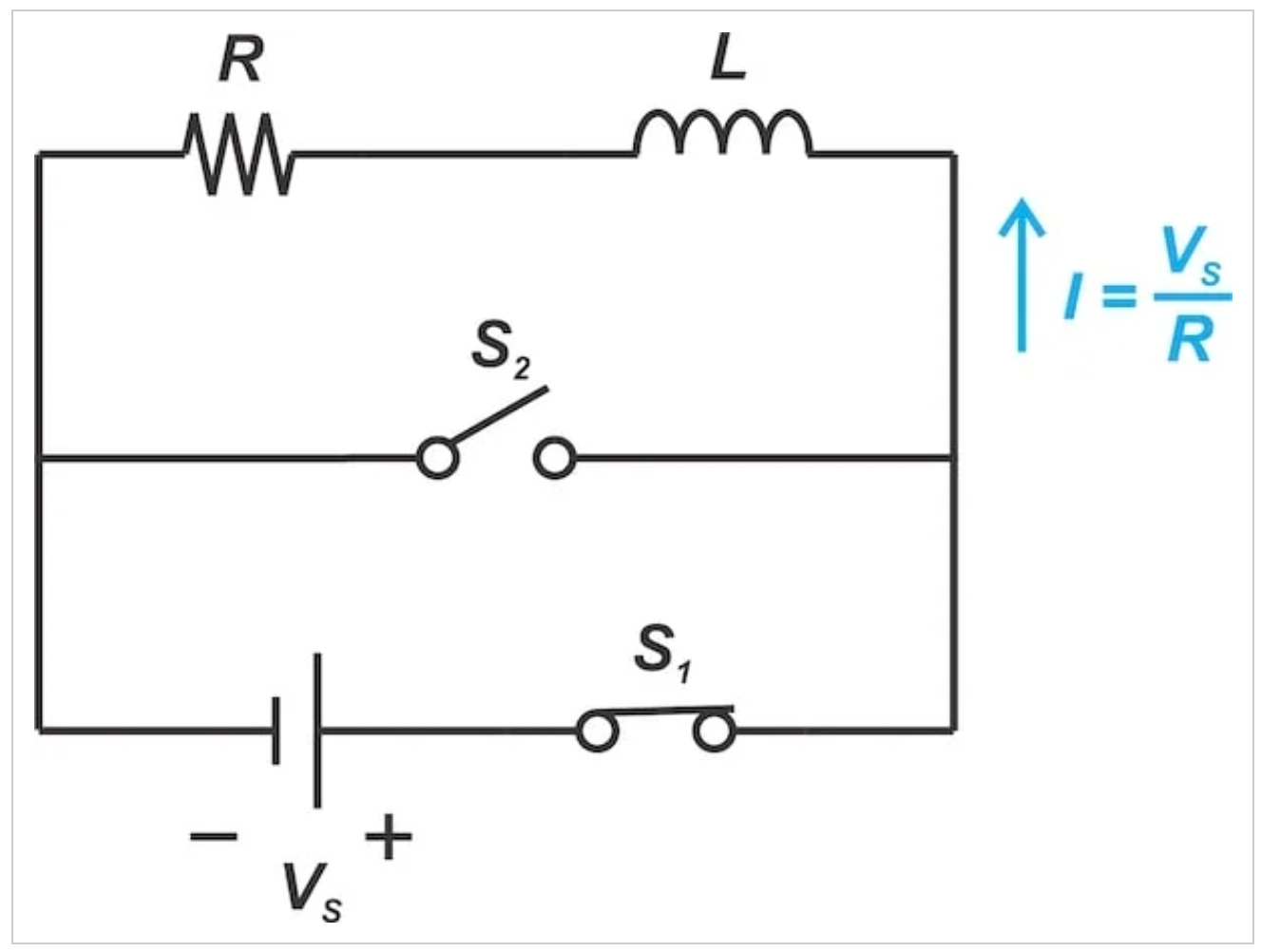
图2:一种理论电路，显示电感器如何释放其初始能量。

该电路包含两个开关S1和S2。它们的操作方式是，当一个开关闭合时，另一个开关打开。

假设S1已经保持闭合足够长的时间，使得流过电感器的电流已经达到其平衡值（I=VS/R）。然后打开S1并关闭S2。这将初始电流为I0=VS/R的电感器连接到电阻器。通过该RL电路的电流是衰减指数，由下式给出：

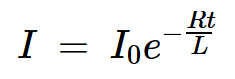
方程式5。

当电流流过RL电路时，RI2的功率被传递到电阻器。将功率在t=0到t=无穷大的范围内进行积分，得到传递给电阻器的总能量。您可以很容易地验证传递到电阻器的总能量等于我们打开S1时存储在电感器中的磁场能量（由方程4给出）。

请记住，这是一个理论上的例子。所有存储的能量都被提供给电路，因为我们假设电感器是无损的。由于磁滞损耗，更不用说涡流损耗等其他损耗机制，现实世界中的电感器会将一些输入能量作为热量耗散。稍后，我们将看到磁滞损耗如何在电感器芯材料的B-H曲线中表现出来。

以磁场量表示的磁能

用磁通密度（B）和磁场强度（H）来表示磁场能量是有帮助的。将磁场从B1变为B2所需的体积能量密度为：

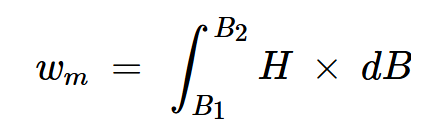
方程式6。

证明上述方程的一般形式相当复杂。然而，对于螺线管或环形线圈等简单结构，我们可以通过应用与方程3中类似的程序来推导方程6。让我们检查一下电磁阀。

螺线管的磁能密度

考虑一个使用磁芯的电磁阀。电磁阀有N圈，长度为l；其核心的磁滞回线如图3所示。

示例螺线管磁芯的磁滞回线。

图3。示例螺线管磁芯的磁滞回线。

如果螺线管的初始磁场强度为h1，那么将磁通密度增加ΔB所需的能量是多少？

我们的第一步是找到在无穷小的时间（Δt）内传递给电感器的瞬时功率：

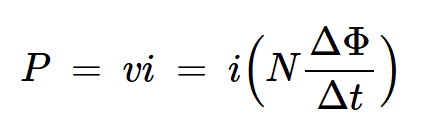
方程式7。

这与方程式1相同，除了电感器电压现在用通过线圈横截面积的磁通量（ɸ）表示。如果横截面积为A，我们有

这将导致：

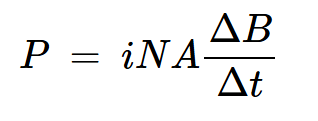
方程式8。

对于具有N匝和长度l的螺线管，磁场强度为H=Ni/l。假设图3中的点a对应于电流i1和场强h1，方程8可以改写为：

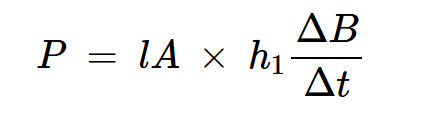
方程式9。

在时间间隔Δt内提供给电感器的增量能量（ΔU）为：

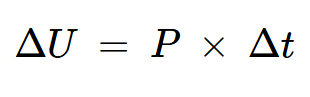
方程式10。

这导致：

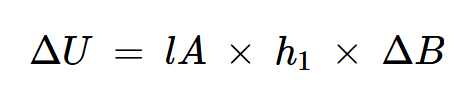
方程式11。

最后，注意lA是螺线管的体积，传递到电感器的增量能量密度为h1×ΔB。这与方程式6一致。

回头参考图3，我们看到传递的能量密度（h1×ΔB）等于阴影条的面积。这是我们计算磁滞损耗所需的关键观察结果。

螺线管磁滞损耗的计算

当向铁磁材料施加正弦磁场时，由于其磁畴的旋转和排列，材料中会耗散一些能量。考虑到这一点，在材料中维持正弦磁场需要多少能量？

让我们考虑图3中磁滞回线周围的一个完整循环，从点f开始，沿着路径fgbcdef回到点f。当我们在磁滞曲线上从点f移动到点g再到点b时，改变磁通密度所需的能量密度等于该路径上（H×dB）的积分。该积分（方程式6）的结果等于图4中的青色面积。

从点f到点b传递到电感器的能量。

图4。从点f到点b传递到电感器的能量。

电流沿着路径fgb增加。因此，能量被传递到电感器。理解这一点的另一种方法是注意，当我们从f移动到B时，H和db（或者，等效地，在短的连续时间间隔中，ΔB）都是正的。

接下来，让我们考虑从b到c的路径。同样，电感器和外部电路之间交换的能量与磁滞曲线和b轴之间的面积成正比。在图5中，该区域为洋红色。

从b点到点c时电感器提供的能量。

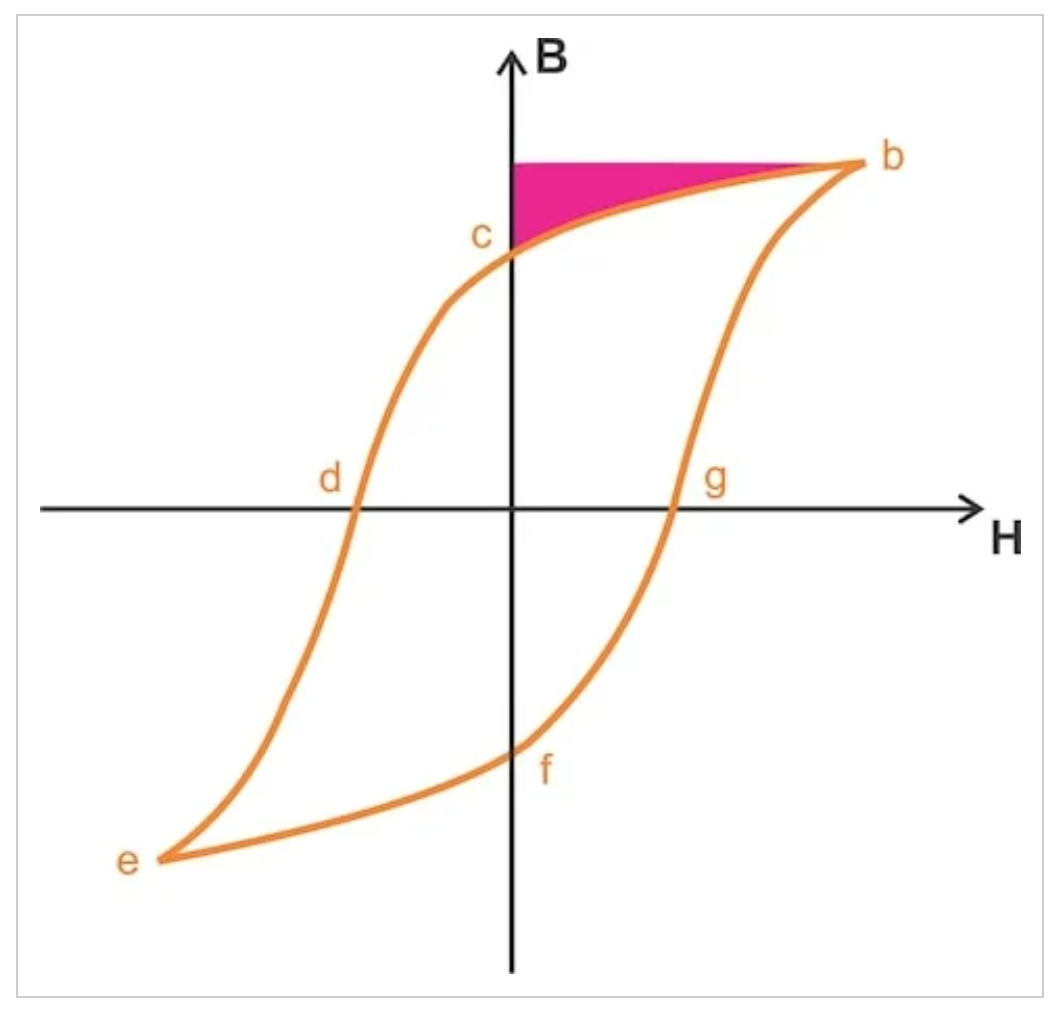
图5。电感器从b点到点c提供的能量。

图中的品红色区域显示了电感器提供的能量，而不是它接收到的能量。在曲线的这一部分，H减小了，因此电感器电流也减小了。电感器正在为外部电路供电。我们还可以得出同样的结论，在这种情况下，H是正的，dB是负的，这意味着传递到电感器的能量是负的。

当我们沿着路径fgbc前进时，传递到电感器的净能量密度是通过从图4中的青色区域减去图5中的品红色区域得到的。这给我们留下了图6中的紫色区域。

沿路径fgbc输送到电感器的净能量。

图6。沿路径fgbc从点f到点c时传递到电感器的净能量。

同样，路径cde的能量对应于图7中的青色区域，路径ef的能量对应图8中的品红色区域。

从点c到点e传递到电感器的能量。

图7。从点c到点e传递到电感器的能量。

电感器从e点到点f提供的能量。

图8。电感器从e点到点f提供的能量。

青色区域再次显示了传递到电感器的能量，品红色区域对应于电感器提供的能量。当我们沿着路径cdef行进时，传递到电感器的净能量密度是通过从青色区域减去品红色区域得到的，从而得到图9中的紫色区域。

沿路径cdef从点c到点f时传递到电感器的净能量。

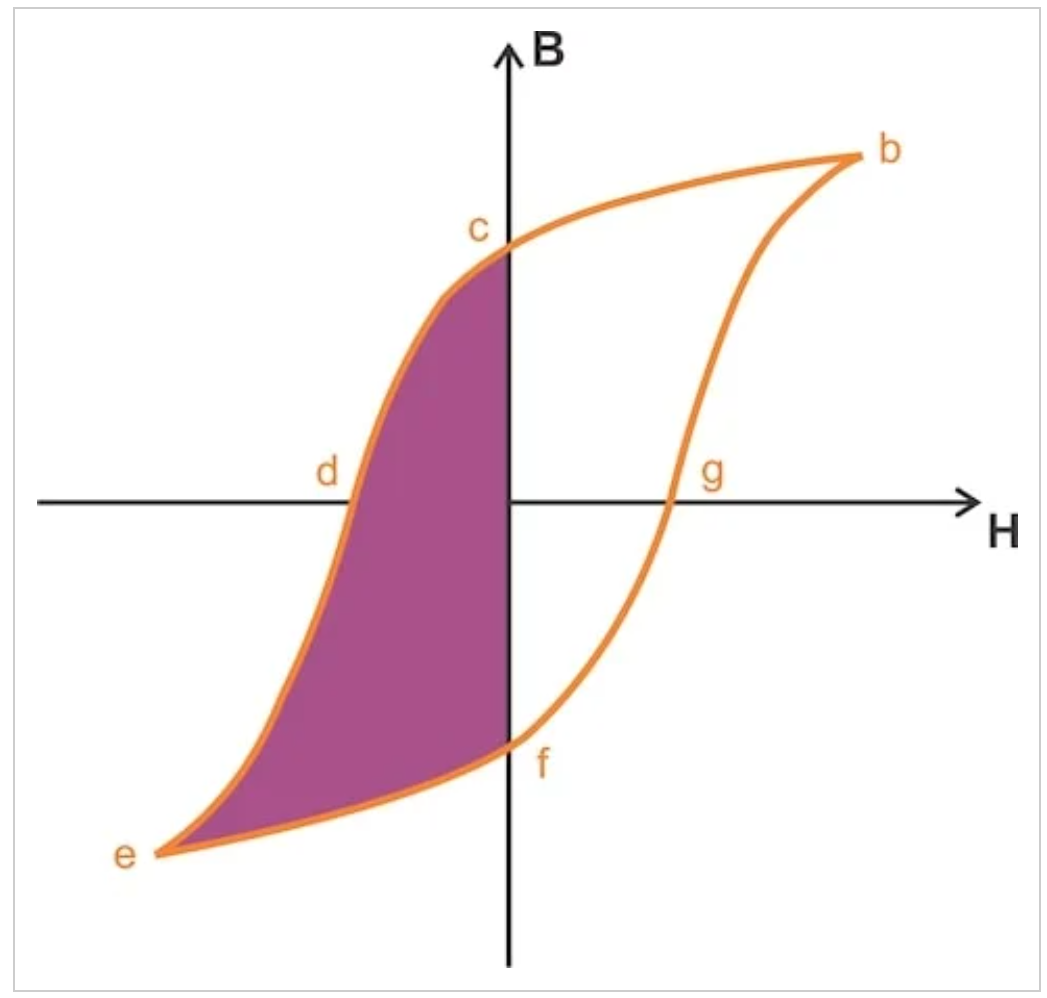
图9。沿路径cdef从点c到点f时传递到电感器的净能量。

总的来说，图6和图9显示了在铁磁材料中维持一个周期的正弦磁场所需的总能量密度。这种能量以热量的形式在材料中消散，等于磁滞回线所包围的面积。滞后面积越大，每个周期的损耗就越大。

通过使用这一关键观察结果，我们可以简单地估计不同材料的磁滞损耗。我们将在本系列的下一篇文章中更详细地讨论这一点，该文章还将介绍一种寻找磁芯磁滞损耗的经验方法。