一种高精度离散时间Σ−Δ调制器的设计*

*基金项目：辽宁省教育厅青年科技人才“育苗”项目，项目编号：LQ2019019

0 引言

随着人们生活水平的不断提高，人们越来越重视自身的健康状况。但人体健康状况的检测无法通过直接观察得到，需要通过精密的医疗仪器对各种信号进行提取如心率、脑电等。人体生物电信号大多为几百赫兹的模拟信号，无法直接对其处理，需要先将其转换为数字信号，所以设计一款应用于低信号带宽的高精度Σ − Δ 调制器是十分必要的^[1]。文献[2]采用五阶一位量化结构，调制器的信噪比为116.5 dB。文献[3]采用MASH2-2结构，调制器的有效位数为17.18 bit。文献[4]采用三阶四位量化器结构，调制器的精度为17.68 bit。目前在低信号带宽下的Σ − Δ 调制器的有效位数大多低于20bit，且高精度调制器结构大多采用三阶以上和多比特量化器的结构。由于单环高阶调制器所以的积分器在同一环路，阶数越高，级联积分器的高频段增益越大，导致系统不稳定。而多比特量化器位数越高，需要的电路越复杂，功耗越大，同时多位的反馈DAC 会降低系统的线性度。本文综合精度、功耗、电路线性度等因素，利用SDToolBox 工具包在Simulink 环境下，设计一款分辨率为24 bit 的三阶一位量化前馈结构的Σ − Δ 调制器，并基于0.18 μm MOS 工艺设计晶体管电路。

1 调制器的行为级建模与仿真

1.1 调制器原理

高阶调制器简易电路框图如图1所示，该调制器由环路滤波器、量化器以及数模转换器构成。其中X (n)为输入信号，Q(n)为量化噪声，Y(n)为调制器的输出。

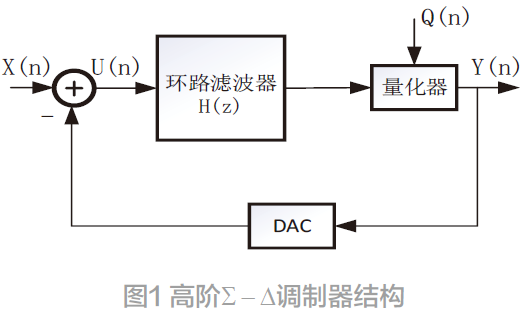
对整个调制器结构进行分析可得：

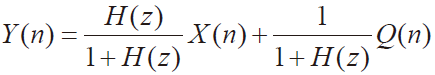
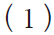
式（1）可知，当 H(z) 足够大时， 而趋于0，输出信号近似等于输入信号，从而最小化量化噪声，提高系统的信噪比。在实际应用中，输入信号频率较低，过采样后大部分的量化噪声位于信号带宽之外，故H(z)为低通特性的滤波器即满足噪声整形要求。

1.2 架构的选择

理论上调制器的最大信噪比为：

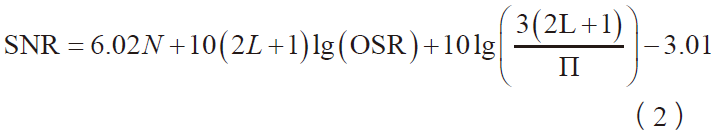
式中，N 为量化位数、OSR 为过采样率、L 为调制器阶数。由式（2）可知使用多位量化器、提高过采样率及采用更高阶调制器可提高调制器的精度。多位量化器可以在低过采样率下获得较高的信噪比，但需要设计额外的数字矫正电路用于消除量化器的非线性，不仅使电路设计更加复杂，还引入了额外功耗。所以本设计采用单bit量化器。根据文献[5] 可知：N 阶单bit 无零极点优化的Σ − Δ 调制器可以实现的最大信号与量化噪声之比（SQNR）值与阶数N 及过采样率OSR 有关，如图2 所示。

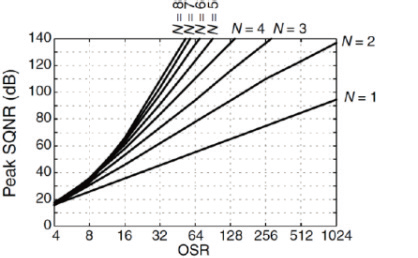
图2 N阶1位调制器的SQNR限制

若调制器的有效位数达到24 bit，则SNR 需达到147 dB。考虑系统的稳定性，采用三阶、过采样率为512 的系统结构。与反馈结构相比，前馈结构的输入信号直接加到量化器的输入端，积分器不含输入信号，因此对积分器的动态范围和线性度要求也相对宽松，非常适合低电源电压使用。设计采用的三阶前馈结构如图3所示。

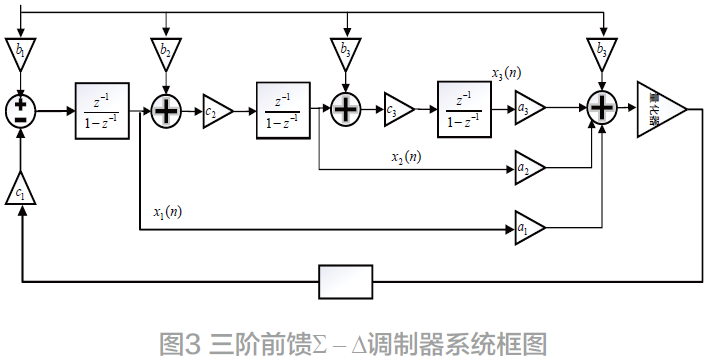
图3 中，a_i,b_i,c_i,x_i(i=1,2,3)为积分器输出的反馈系数，输入前馈系数，积分器增益系数和积分器的输出。

1.3 系数的确定

使用SDToolBox 包中的synthesizeNTF 函数得到初始的噪声传递函数，具体使用方式如下：

NTF = synthesizeNTF(order = 3,osr = 512,0,H_{_ inf}=1.5,0) 

order：调制器的阶数，osr ：过采样率，H_{_ inf} ：NTF的最大带外增益。根据Lee 准则^[6]，NTF在所有频率上的最大增益小于1.5，则一位量化调制器多半是稳定的，故H_{_inf}=1.5。使用realizeNTF辅助函数求出相关系数，省去繁琐的计算过程。由于比例系数决定电容值的比，因此在设计时需要考虑电路级设计中较为容易实现的电容值比并确保积分器的输出摆幅在预期范围内。若第1级积分器的输出摆幅过大，则需要将第1 级积分器的增益系数减小为原来的以此来降低第1 级积分器的输出摆幅。同时为了确保传递函数及x₂保持不变，需将后模块的系数需要放大至原来的x倍。通过scaleABCD函数对综合后的参数进行动态范围缩放，再经反复仿真验证，调制器系数如表1 所示。

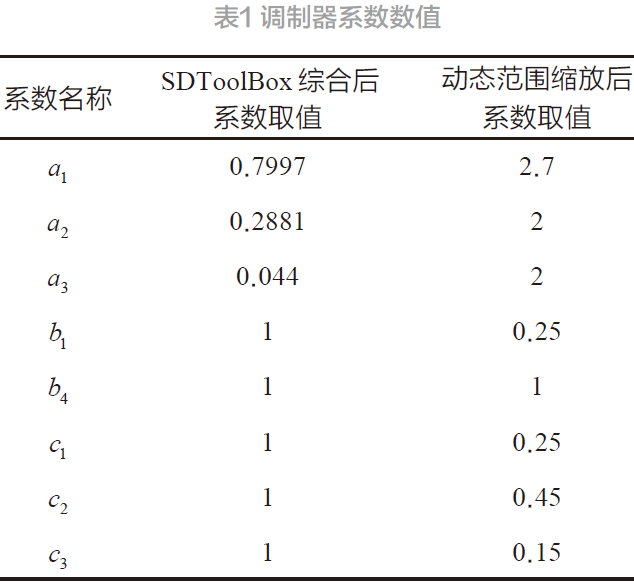
进一步考虑动态缩放后系数值的可行性，将系数值代入到系统中，利用SDToolBox 工具包对系统的稳定性进行分析，得到的结果如图4 所示。由图4 可知，z = 1 时，有1 个零点且3 个极点的位置均在单位圆内，该系统是稳定的。

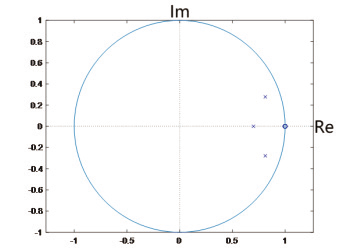
图4 零极点分布

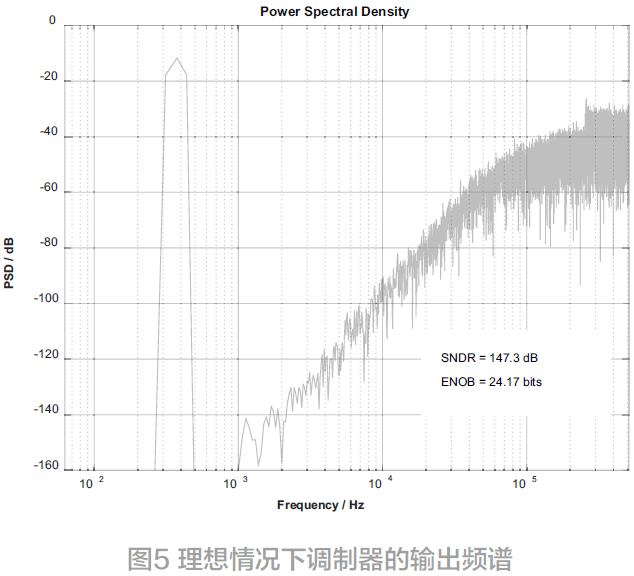
理想情况下调制器输出的频谱图如图5所示。当输入信号幅度为0.45 V 时，调制器的有效位数为24.17 bit，满足设计要求。

1.4 非理想化建模

对非理想化因素如时钟抖动、开关热噪声、运放的非线性和噪声等进行建模验证电路性能。

1.4.1 时钟抖动

Σ − Δ调制器主要是由开关电容电路构成，而开关电容电路是通过控制时钟的高低电平的转换完成采样和积分操作。时钟的电平变化不是立即完成的，存在时钟抖动现象。时钟抖动现象会直接导致均匀的周期性采样变得非均匀。设输入信号是幅度为A，频率为f_in的正弦波，时间偏差范围为[−δ，δ ]，其时钟抖动^[6]：

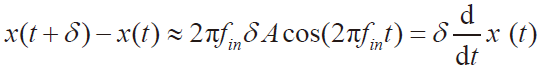
加入时钟抖动模型，得到在不同时钟抖动下，调制器的SNR 如图6 所示。

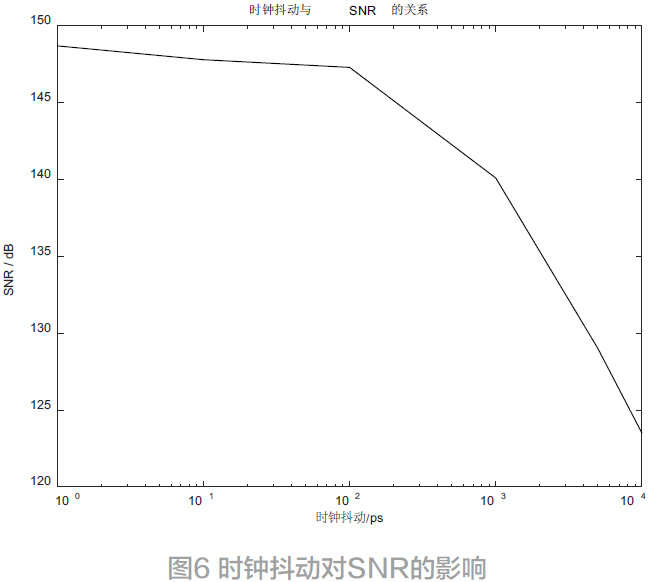
时钟抖动对SNR 的影响有限，即使时钟抖动高达1 000 ps，调制器的SNR 仅下降了7 dB。

1.4.2 KT/C热噪声

开关热噪声是影响调制器性能的重要因素，而开关电容电路的热噪声主要是由采样电容决定的。第一级积分器的采样电容决定了调制器的噪声底板，其等效热噪声^[8]为

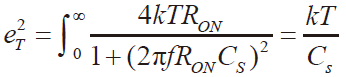
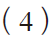
式中， k为玻尔兹曼常数；T为绝对温度； c_s为采样电容。加入KT/C热噪声模型，得到采样电容对调制器性能的影响如图7 所示。

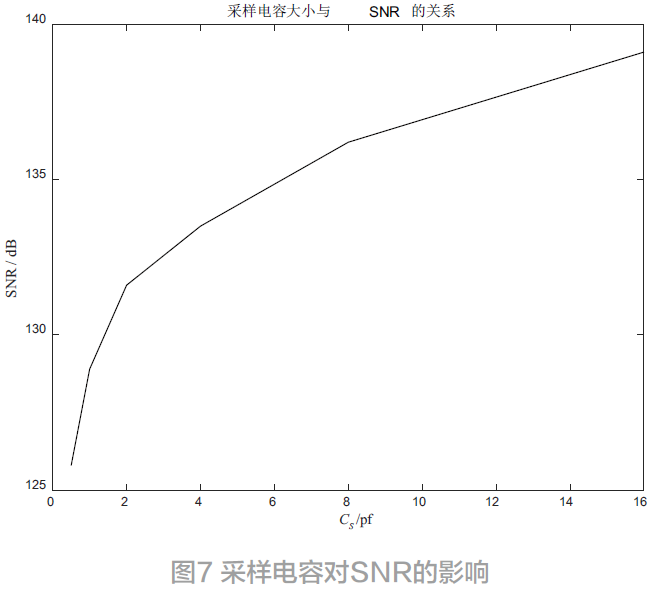
由图7 可知，采样电容为4 pf 时，调制器的SNDR下降至136 dB。增加采样电容至16 pf，调制器的SNR为139 dB 并没有太大的提高，反而会增加芯片面积、增加运算放大器的设计难度。

1.4.3 运算放大器的非理想因素

运算放大器是积分器的核心模块，其性能决定了整个调制器所能达到的最高指标。运算放大器的非理想因素包含有限增益、有限带宽与输出摆幅、压摆率和噪声等。由于有限直流增益的影响，采样电容中的电荷无法完全转移到积分电容中，积分器发生电荷泄漏，从而改变信号传递函数的极点位置，造成系统的不稳定。而有限的单位增益带宽会影响小信号的建立时间，在第n 个积分周期，开关电容型积分器的输出电压为：

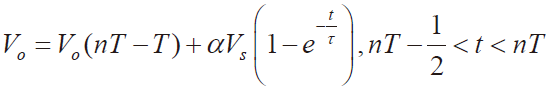
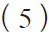
式（5）中，α 与积分泄露有关；τ 为积分器的时间常数，与运算放大器的单位增益带宽有关。图8 是不同增益下，调制器信噪比的情况。

根据图8 可知，在运算放大器的直流增益大于60 db，调制器的SNR 稳定在140 dB 以上。

1.5 Simulink仿真

对上述的非理想因素进行仿真。通过反复仿真验证，确定的参数如表2 所示。

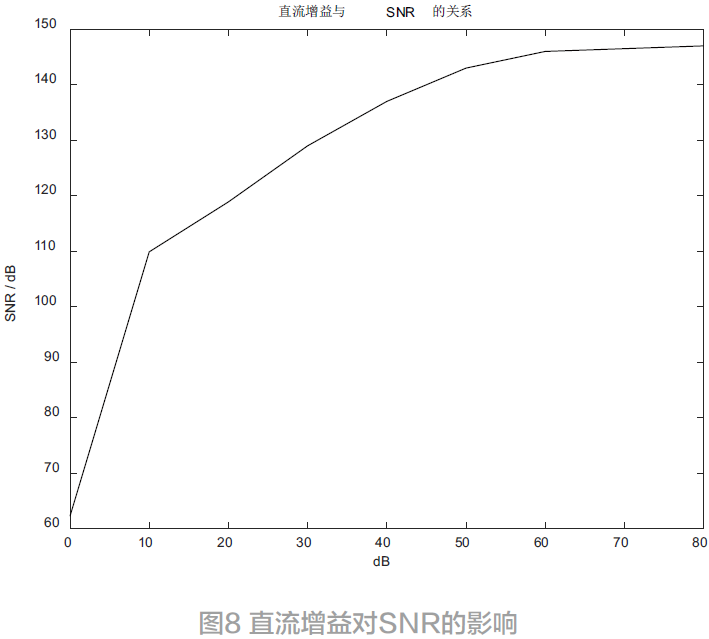
考虑非理想因素时，三阶调制器的输出频谱如图9所示。SNDR为135.6 dB， 调制器的有效位数为22.23 bit。

2 cadence下晶体管级电路的设计与仿真

2.1 电路设计

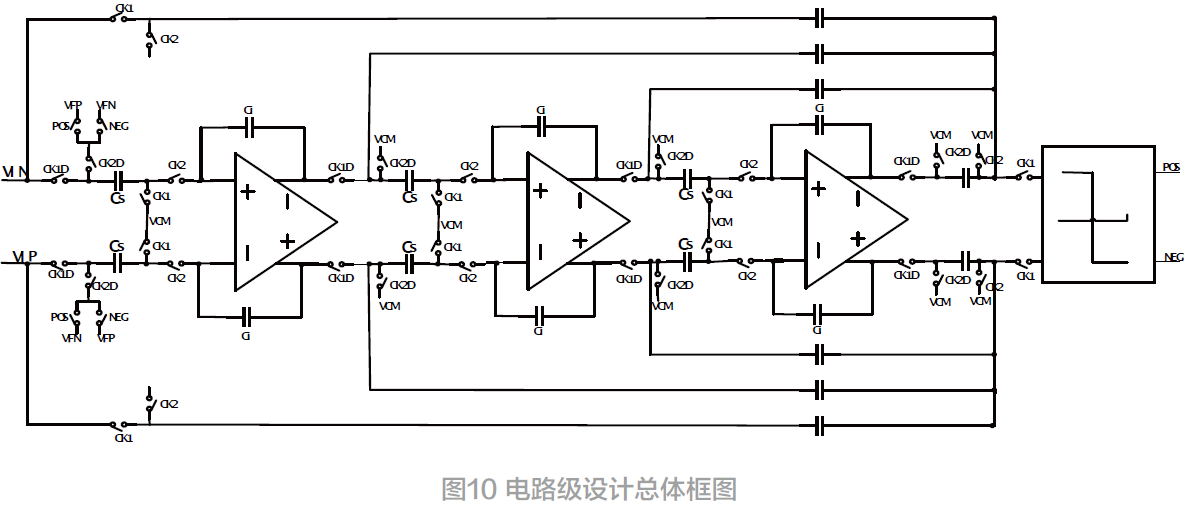
采用开关电容电路实现的单环三阶一位量化Σ − Δ调制器整体框图如图10 所示。整个电路系统工作在两项非交叠时钟下，为了降低沟道电荷注入效应，对CK1、CK2 进行延时CK1D、CK2D。当CK1 为高电平、CK2 为低电平时，系统工作在采样状态；CK2 为高电平、CK1 为低电平时，系统工作在积分状态。

2.1.1 全差分放大器

基于0.18 μm CMOS 工艺设计电路。根据表2 中非理想取值可知，积分器中的运算放大器需要60 dB 以上的直流增益来满足精度要求。单极共源共栅结构运算放大器相比两级运算放大器没有那么高的直流增益，但也能轻松到达60 dB 的增益，前者有着更大的增益带宽积，后者会引入额外的零极点，导致电路系统的不稳定。而折叠式共源共栅放大器相较于套筒式结构，有着较大输入共模范围和输出摆幅，且输入电压范围和输出电压范围没有关联，故采用折叠式共源共栅放大器结构，具体结构如图11 所示。

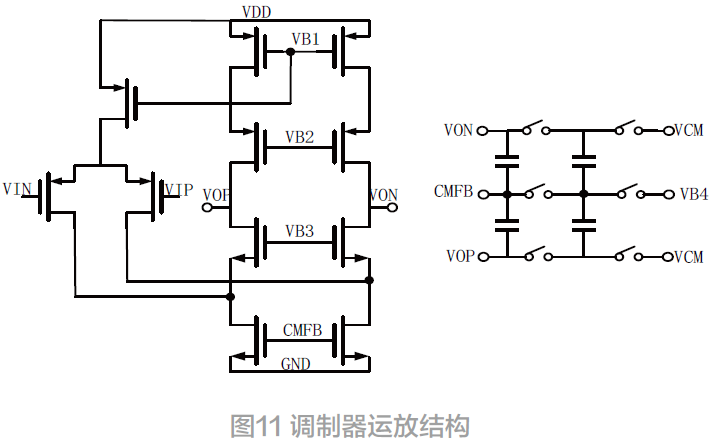
图11 中左边部分为折叠共源共栅的电路结构，右边为开关电容共模反馈。开关电容共模反馈电路控制运放的输出共模电压，以获得较大的动态范围。同时开关电容共模反馈和开关电容积分器使用同一个时钟，不需要额外设计时钟，简化了电路结构。图12 为全差分运算放大器在不同温度与工艺角下的幅频特性曲线图。

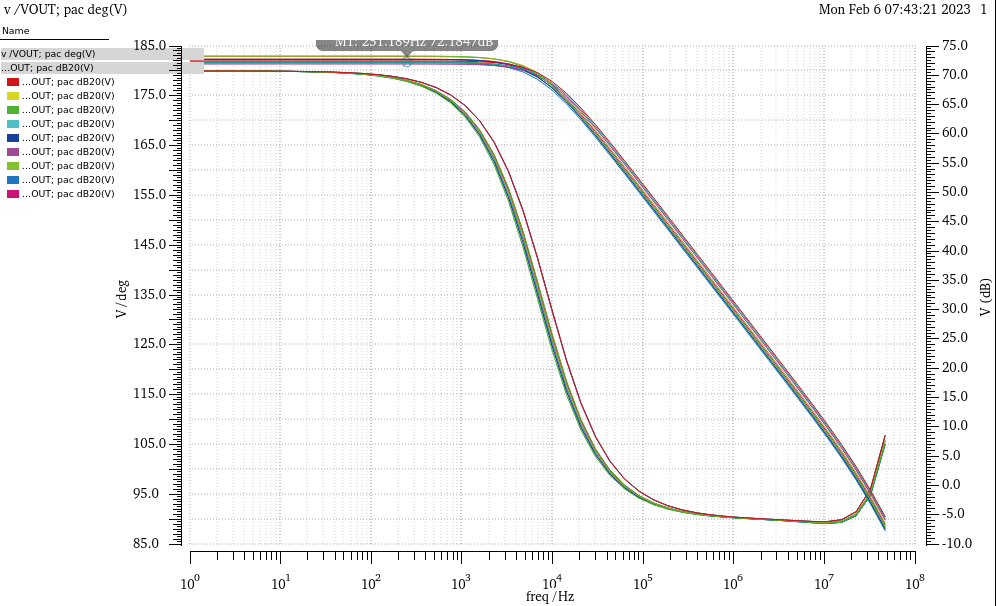
图12 运算放大器幅频特性仿真结果

运算放大器的直流增益为72 dB 以上，增益带宽积为15 MHz 以上，相位裕度为88° 。

2.1.2 量化器

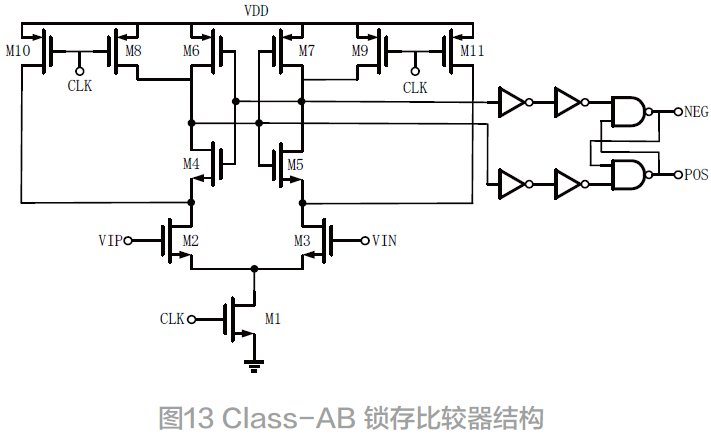
Σ − Δ调制器的噪声整形技术会对量化器的非理想因素进行处理，因此对量化器的性能要求并不高。一位量化器采用速度快、功耗低的Class-AB 锁存比较器和SR锁存器，其结构如图13 所示。当CLK 为低电平时，比较器处于复位状态。当CLK 为高电平时，比较器处于比较状态。

2.2 仿真结果

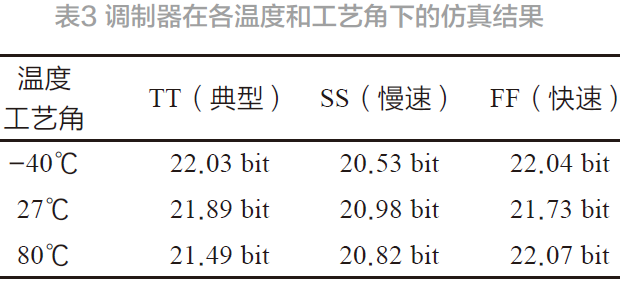
使用spectre 仿真工具进行瞬态仿真，将仿真结果导入Matlab 的PSD 模块计算结果。输入信号幅度为0.5 V、频率为375 Hz、过采样率为512 GSa/s，在不同温度与工艺角下，调制器的信噪比结果如下表3。

在常温和TT 工艺角下，电路仿真结果如图14 所示。调制器的信噪比为133.5 dB，有效位数为21.89 bit。

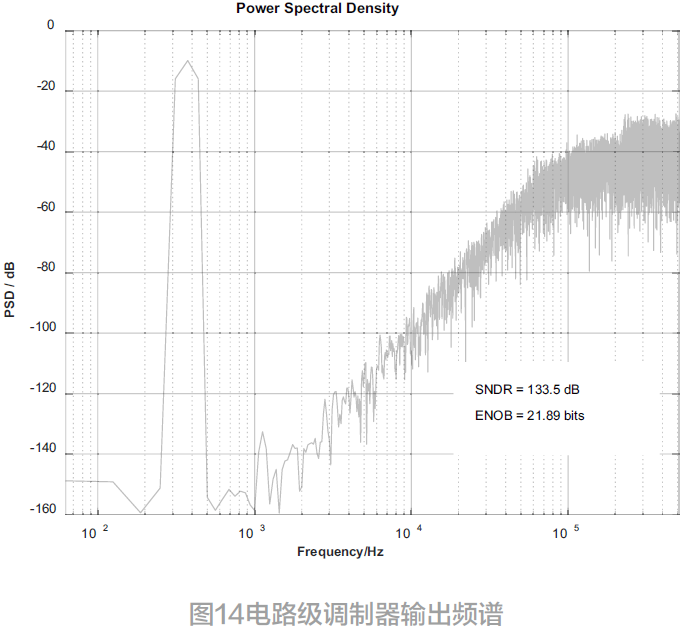
2.3 结果对比

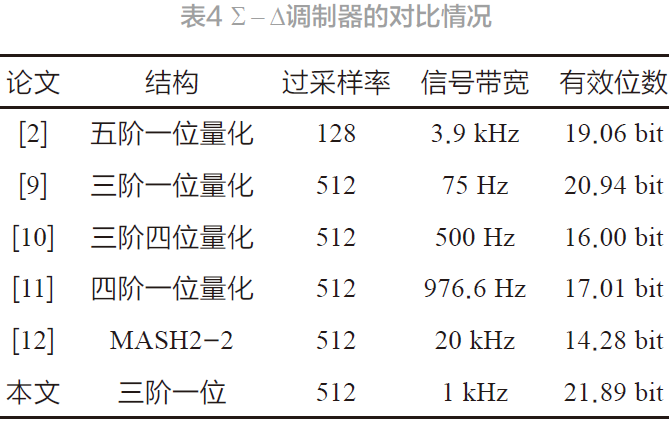
表4 为近几年国外内设计的低信号带宽下Σ − Δ 调制器的对比情况。由表可知：本文在未采用三阶以上结构及多位量化器的情况下，仅采用最简单的三阶一位量化器结构，就实现了21.89 bit 的有效位数，大大地降低了电路设计的复杂性。

3 结束语

本文设计了一款信号带宽为1 kHz 的单环三阶一位量化前馈结构的Σ − Δ 调制器。进行了非理想因素的行为级仿真，确定电路子模块的性能参数。在1.8 V 电源电压下，采用0.18 μm CMOS 工艺实现晶体管级电路设计。仿真结果表明：电路的有效位数为21.89 bit，实现了低信号带宽场合下的高精度转换。可广泛应用于心电图测量、脑电图测量等医疗领域。

参考文献：

[1] 张笑天. 基于传感应用的高精度sigma-delta模数转换器的关键技术研究与设计[D].西安:西安电子科技大学,2021.

[2] 李明昊,杨拥军,任臣,等.应用于MEMS惯性器件的高精度Σ-Δ调制器[J].半导体技术,2021,46(12):926-931.

[3] 沈晓峰,李梁,付东兵,等.基于MASH结构的24 bit Σ-Δ A/D转换器[J].微电子学,2022,52(2):223-228.

[4] 李春斌. 24 bit-2 kHz高精度Sigma-Delta调制器系统设计与研究[D].西安:西安电子科技大学,2021.

[5] R. SCHREIER. An empirical study of high-order singlebit delta-sigma modulators[J]. IEEE Transactions on Circuits and Systems I Regular Papers,1993,40(8).

[6] G YIN, W SANSEN. A high-frequency and highresolution fourth-order Sigma-Delta A/D converter in BiCMOS technology[J].IEEE Journal of Solid-State Circuits,29:857-865,August 1994.

[7] NDJOUNCHET. Delta-sigma data converters [M]. BocaRaton:CRCPress, 2011.

[8] SCHREIER R. An empirical study of high-order single-bit delta- sigma modulators [J]. IEEE transactions on circuits and systems II:analog and digital signal processing,1993,40(8):461-466.

[9] 尹勇生,邓春菲,陈红梅.高精度Sigma-Delta调制器的建模设计[J].微电子学与计算机,2016,33(5):28-32.

[10] BAI W, WANG Y, ZHU Z. A 0.8-V 1.7-μW25.9-fJ continuous-time Sigma-delta modulator for biomedical a p p l i c a t i o n s [ C ] / / B i o m e d i c a l C i r c u i t s a n d S y s t e m s Conference. IEEE， 2017:248-251.

[11] 王冠然. 低速高精度Sigma-Delta调制器的研究与设计[D].大连:大连理工大学,2021.

[12] SUNG G M, LEE C T, XIAO X, et al. 4 th-Order Switched-Current Multistage-Noise-Shaping Delta-Sigma Modulator With a Simplified Digital Noise-Cancellation Circuit[J]. IEEE Access,2020,8:168589-168600.

（本文来源于必威娱乐平台 杂志2023年5月期）