一种使用Python来分析混合模式信号链中噪声的简单方法

简介

混合模式信号链无处不在。简单地说，任何将真实世界的信号转换为电子表示（然后数字化）的系统都可以被归类为混合模式信号链。在信号链的每个点上，信号都以各种方式降级，从特征来看，可能是出现一定程度的失真，或是出现相加噪声。在进入数字领域之后，对数字化数据的处理也不是完美的，但至少，实际上可以不受许多影响模拟信号的因素的影响——部件公差、温度漂移、邻近信号的干扰或电源电压变化。

随着行业不断扩展物理限制，有一点是肯定的：仪器仪表的模拟和混合信号部件始终存在可改进的空间。如果市场上出现的模数转换器(ADC)或数模转换器(DAC)在速度、噪音、功率、精度或价格方面都表现出色，制造商会很乐意用其来解决现有问题，然后要求进行更多改进。但是，为了给客户应用提供最佳的采集系统，就必须了解每种部件的限制，然后做出相应选择。

本教程ADI将侧重介绍单个信号链元件的噪声，（可视作转换器连接教程的续篇^1,2），并使用Python/SciPy³和LTspice^®来模拟这些噪声。然后，使用Python，通过libm2k和Linux^®工业输入输出(IIO)框架来驱动ADALM2000多功能测试仪器来验证模拟结果。关于源代码和更多讨论，请参见配套的主动学习实验室练习。

一种通用的混合模式信号链

图1显示了在精密仪器应用中很典型的一种通用信号链，提供物理输入和数字输出。目前有许多关于ADC的背景参考资料⁴，大部分读者都知道，ADC会在某个时点对输入信号进行采样（或测量某个观察时间段内信号的平均值），并生成该信号的数值表示，通常是二进制数值，其值介于0和2(N – 1)之间，N表示输出字的位数。

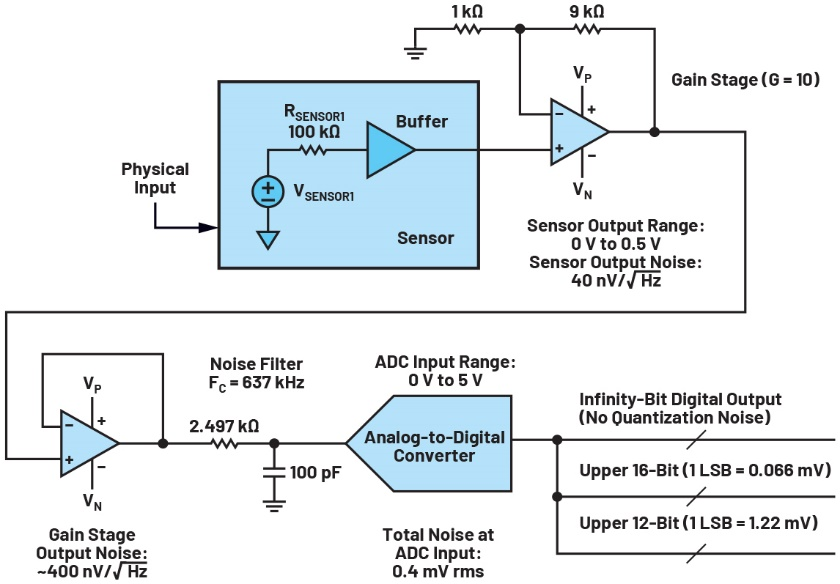
图1 在混合模式信号链中，会将一些物理现象（例如温度、光强度、pH值、力或扭矩）转换为电气参数（电阻、电流或直接转换为电压）。然后，该信号被放大，受到低通滤波，然后被ADC数字化，ADC中可能包含内部数字滤波

ADC噪声源

虽然图1中有多个噪声源，但有一个经常被忽略，或是被过分强调，即ADC数字输出的位数。以前，人们将ADC的位数视为评断品质的终极指标，认为16位转换器比14位转换器好出4倍。⁵但在现在的高分辨率转换器中，位数几乎可以忽略。注意，信号链设计要奉行一条一般原则：“某一级的输入噪声应在一定程度上低于前一级的输出噪声。”

与信号链一样，ADC内部通常也有一个噪声源占主导。所以，如果对N位ADC应用无噪声信号：

■   要么得出单个输出代码，要么得出两个相邻的输出代码，然后量化噪声占主导地位。信噪比(SNR)不会大于(6.02N + 1.76)dB。⁶

■   多个输出代码呈高斯分布，热噪声源占主导地位。SNR不会大于：

其中：V_IN(p-p)表示满量程输入信号。α表示以电压为单位的输出代码的标准偏差。

分辨率很高的转换器（例如AD7124-8，稍后会用作示例）很少受量化噪声限制；在所有增益/带宽设置中，热噪声占主导地位，短路输入始终会导致产生按高斯分布分布的输出代码。图2显示24位Σ-Δ ADC AD7124-8的接地输入直方图，内部可编程增益放大器(PGA)分别设置为1和128。

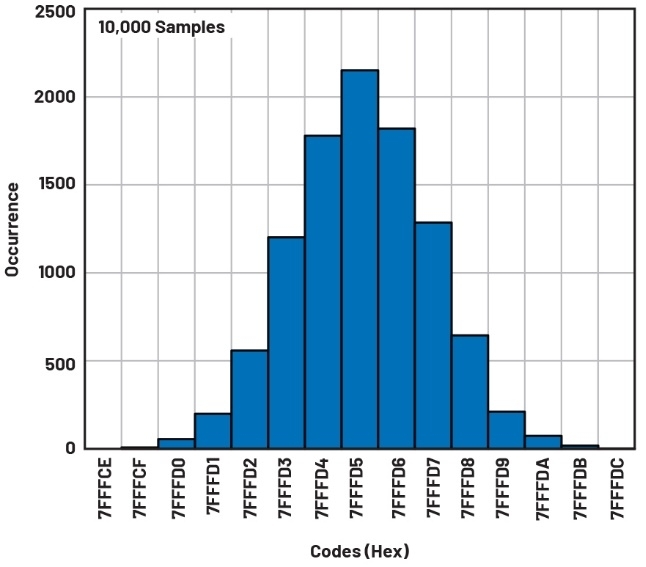
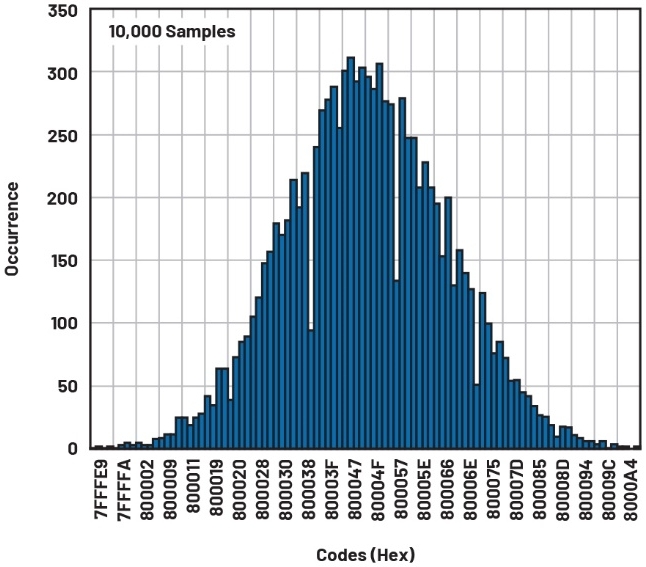
图2 在PGA增益为1时（左侧），AD7124输出噪声中显示13个代码，标准偏差为约2.5个代码。当量化噪声可见时，热噪声更为显著。在PGA增益为128时（右侧），显示187个代码，量化噪声是无关紧要的。截断一个或两个最低有效位（双倍或四倍量化噪声）不会导致信息丢失

模拟和测量ADC噪声

模拟热噪声受限的ADC的噪声是很简单的。如果噪声“表现正常”（如图2所示，呈高斯分布），且在ADC的输入范围内保持恒定，即可使用NumPy⁷的随机正常函数来模拟ADC的时域噪声，然后通过标准偏差来进行验证，如图3所示。

图3 使用NumPy模拟高斯噪声

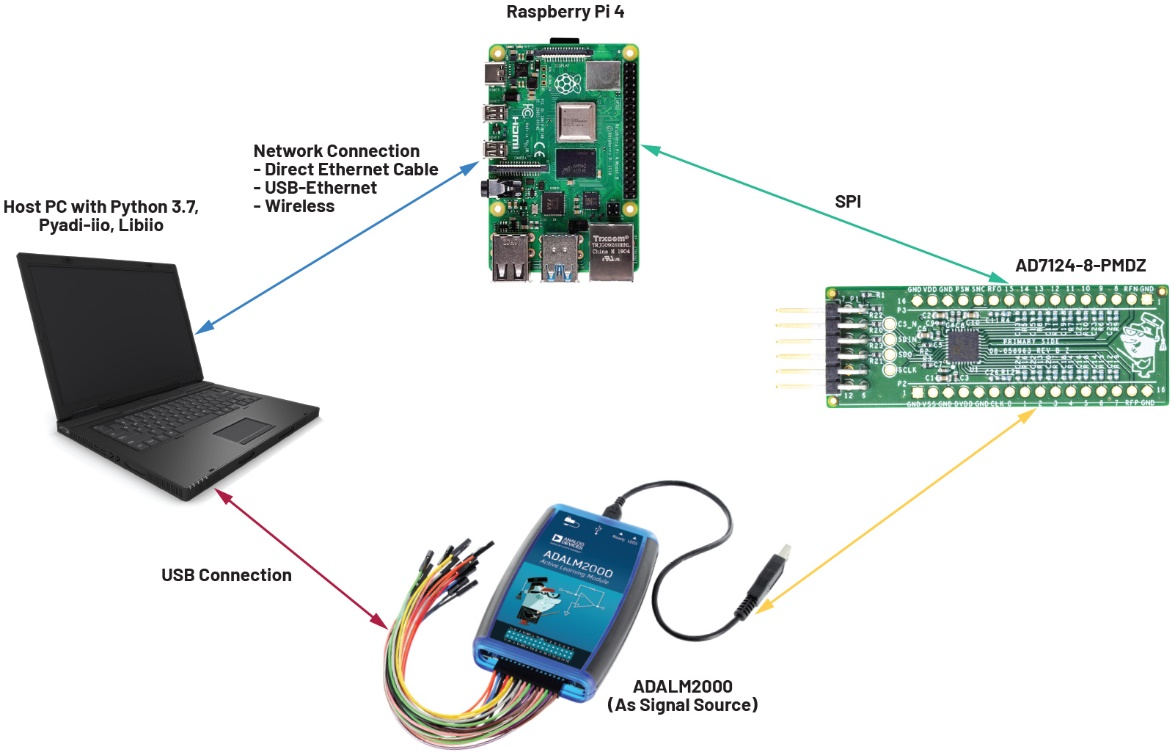
图4 ADALM2000是一款多功能USB测试仪器，具有两个通用模拟输入和两个输出，采样率分别为100 MSPS和150 MSPS。它可以作为简单的信号源，用于测量ADC噪声带宽和滤波器响应。运行支持AD7124器件驱动器支持的内核的树莓派4作为AD7124和主机之间的简单桥梁

AD7124设备驱动器在行业标准IIO框架之内，该框架具有完善的软件API（包括Python捆绑）。应用代码可以在本地（在树莓派上）运行，也可以通过网络、串行或USB连接在远程机器上运行。此外，pyadi-iio8抽象层负责与IIO器件进行连接所需的大部分样板的设置，极大地简化了软件接口。图5显示如何打开AD7124-8的连接，进行配置，捕捉一个数据块，然后关闭连接。

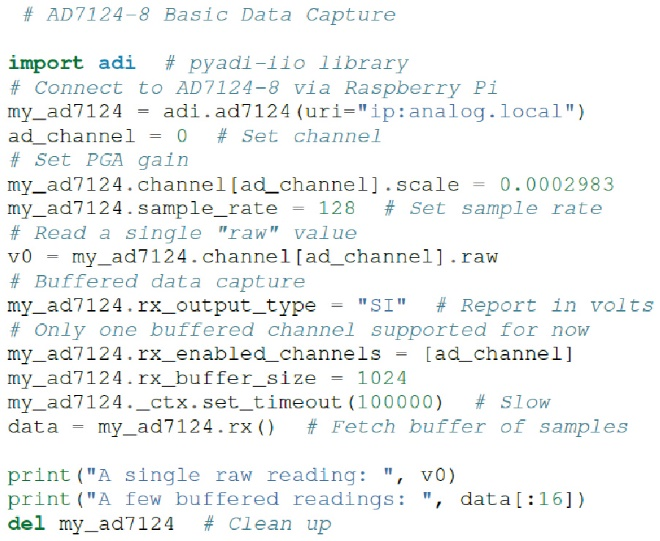
图5 AD7124-8基本数据捕捉

建立与AD7124-8的通信之后，可以执行非常简单，但非常有用的测试：直接测量输入噪声。简单地让ADC的输入短路，然后查看ADC代码的分布，这是确定信号链设计的一个非常有用的步骤。AD7124的输入模式设置为单极性，所以只有正值是有效的；图6所示的测试电路确保输入始终为正值。

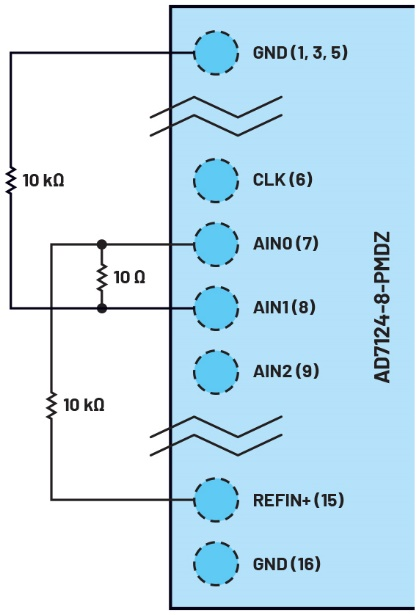
图6 使用一个电阻分压器在AD7124-8的输入中生成1.25mV偏置，克服15µV最大失调电压，确保ADC的读数始终为正

图7显示两个1024点的测量值。下方的（蓝色）线条是在初次通电后立即获取的。

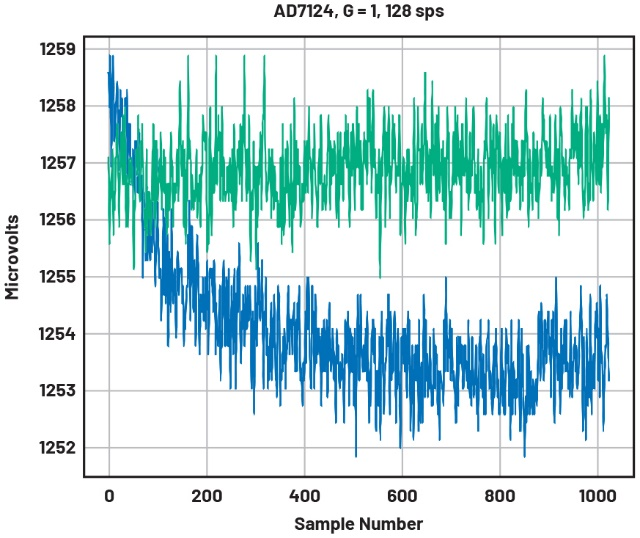
图7 两次AD7124-8数据捕捉是在采用1.25mV偏置的情况下进行的。下面的线条显示在通电后，电路升温时的初始漂移。上面的线条显示在半个小时升温后，读数达到稳定

“漂移”可能是由许多因素造成的——内部基准电压源升温、外部电阻升温（因此漂移），或者是因为寄生热电偶，在热电偶中，稍微不同的金属会在存在热梯度的情况下产生电压。升温后测量到的噪声为约565nV rms，与数据手册中的噪声规格相当。

用密度表示ADC噪声

如果所有元件都包括噪声密度规格（大部分明确规定的传感器和几乎所有的放大器都如此要求），模拟信号链设计的一般原则（某一级的输入噪声应在一定程度上低于前一级的输出噪声）将是一项简单的计算。

与放大器和传感器不同，ADC数据手册通常不包括噪声密度规格。用密度表示ADC的噪声之后，可以直接与模拟信号链的最后一个元件的输出噪声进行比较，它可能是ADC驱动器级，是增益级，或是传感器本身。

ADC的内部噪声必然会出现在DC和采样率的一半之间。理想情况下，该噪声是扁平的，或者至少是可预测的形状。事实上，由于ADC的总噪声分布在已知带宽上，所以可以将其转换成噪声密度，然后直接与信号链的其他元件进行比较。精密转换器的总噪声通常会直接给出，单位为Vrms：

其中eRMS表示总有效值噪声，根据代码的接地输入直方图的标准偏差进行计算。

用正弦信号测试和表征的更高速度的转换器通常包含SNR规格。如果提供，可使用以下公式计算总有效值噪声：

其中ADCp-p是ADC的峰峰值输入范围。可以使用以下公式计算等效噪声密度：

其中fS表示ADC采样速率，单位为样本/秒。

在128SPS的数据速率下，在升温后图7的总噪声为565nV。噪声密度约为：

ADC现在可以直接纳入信号链噪声分析中，为优化信号链增益提供了指导。

■   增加增益，只要到达“ADC之前的最后一个级的噪声密度比ADC的噪声密度高一位”的点，即停止。切勿再增加信号链增益——这只会放大噪声，并减小允许的输入范围。

这与“填补”ADC的输入范围的传统智慧背道而驰。如果ADC的转换函数中存在步进或断续，超出ADC的输入范围可能会有好处，但对于“表现正常”的ADC（大多数Σ-Δ ADC和现代的高分辨率逐次逼近寄存器(SAR) ADC）来说，通过噪声进行优化是首选方法。

测量ADC滤波器响应

AD7124-8是一个Σ-Δ ADC，其中调制解调器产生高采样率，但噪声大（低分辨率），表示模拟输入。这些噪声很大的数据然后被内部数字滤波器过滤，产生更低速率、更低噪声的输出。滤波器的类型因ADC而异，具体由预期的最终应用决定。AD7124-8是针对精密应用的通用器件。因此，数字滤波器响应和输出数据速率是高度可配置的。虽然数据手册中明确定义了滤波器响应，但有时可能需要测量滤波器对给定信号的影响。AD7124-8滤波器响应代码块（参见图9）通过将正弦波应用到ADC输入并分析输出来测量滤波器响应。该方法适用性高，可用于测量其他波形——子波和模拟的物理事件。ADALM2000连接至AD7124-8电路，如图8所示。

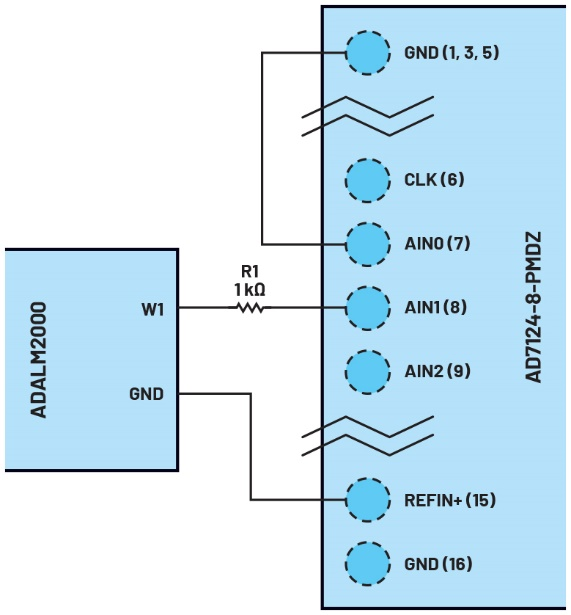
图8 ADALM2000波形发生器用于生成一定范围的正弦波频率，以直接测量AD7124-8的滤波器响应。虽然脚本将正弦波幅度和偏移设置为安全水平，1kΩ电阻可以在功能故障时保护AD7124-8。（ADALM2000的输出电压范围为–5V至+5V，而AD7124-8的绝对最大限值为-0.3V和+3.6V。）

AD7124-8滤波器响应代码块（参见图9）将设置ADALM2000的波形发生器，生成10Hz正弦波，捕捉1024个数据点，计算rms值，然后将结果附加到列表中。send_sinewave和capture_data是实用函数，分别用于发送一个正弦波到ADALM2000和接收来自AD7124的数据块。2 接着，它将频率步进增加，直到达到120Hz，然后给出图10所示的结果。

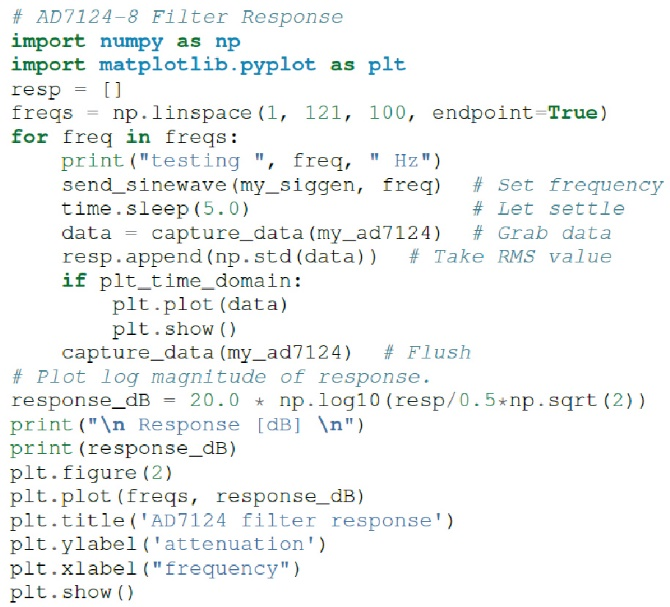
图9 ADALM2000的滤波器响应框图

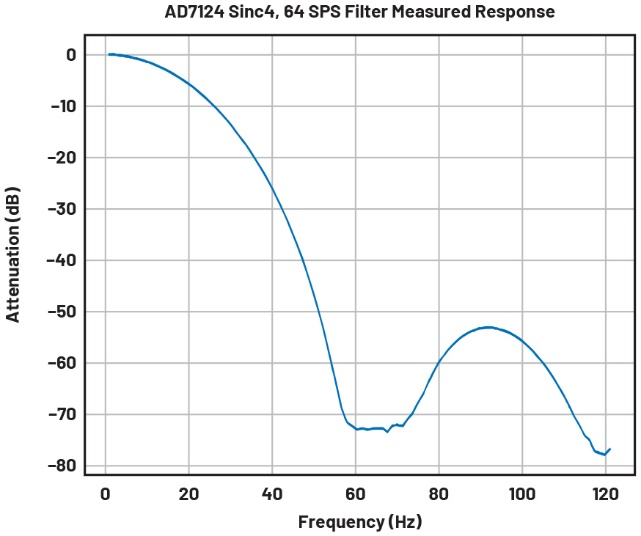
图10 在64 SPS、sinc4模式下测量AD7124滤波器的响应，显示滤波器的通带、第一个波瓣和前两个零位

当测量高衰减值需要一个更安静和更低失真的信号发生器时，在此设置下，前几个主要波瓣的响应是明显的。

模拟ADC滤波器

测量ADC的滤波器响应的能力是一项实用的平台验证工具。但是，要完全模拟信号链，需要滤波器的模型。关于这一点，许多转换器（包括AD7124-8）没有明确指明，但可以根据数据手册中提供的信息逆向设计得出可用的模型。

注意，以下只是AD7124-8滤波器的模型；不是位精准的表示。请参考AD7124-8数据手册查看所有保证参数。

AD7124的滤波器都具有由各种sinc函数组成的频率响应（频率响应与(sin{f}/f)N成正比）。这些滤波器易于构建，在零位已知的情况下可以逆向设计。

图11显示AD7124-8的10Hz陷波滤波器。还提供高阶sinc3和sinc4滤波器的各种组合。

滤波器的脉冲（时域）形状如图14所示。滤波器系数(tap)值被标准化，以得出零频率时的单位(0dB)增益。

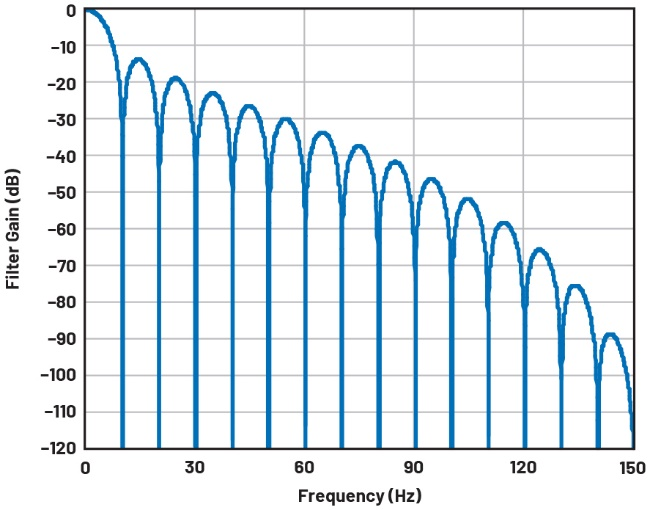
图11 AD7124-8 10 Hz陷波滤波器具有sinc1幅度响应；滤波器的脉冲响应只是100 ms时间间隔内样本的未加权（矩形）平均值

图12中显示的同步50Hz/60Hz拒波滤波器是一个重要示例。此滤波器用于强烈抑制来自交流电源线的噪声，可能是50Hz（与欧洲一样），或者是60Hz（与美国一样）。

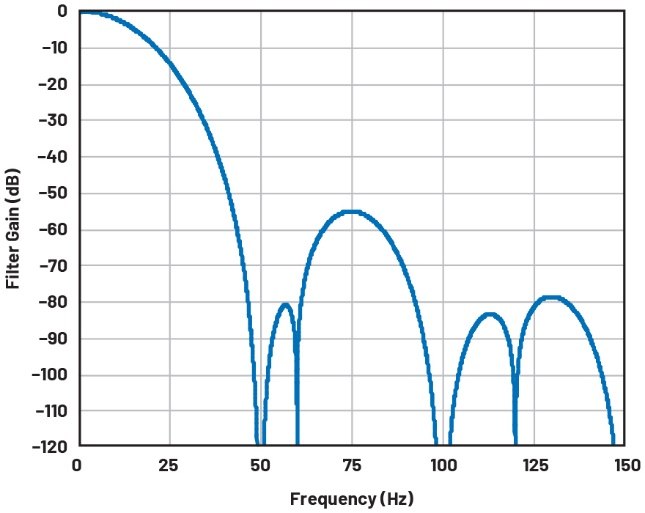
图12 AD7124-8 50Hz/60Hz拒波滤波器响应是50Hz sinc3滤波器和60Hz sinc1滤波器的组合

可以通过对sinc1滤波器进行卷积来生成更高阶的sinc滤波器。例如，将两个sinc1滤波器（在时间上有一个矩形脉冲响应）进行卷积将得到一个三角脉冲响应和一个相应的sinc2频率响应。AD7124滤波器代码块（参见图13）生成一个sinc3滤波器，在50Hz时为零，然后添加第四个滤波器，在60Hz时为零。

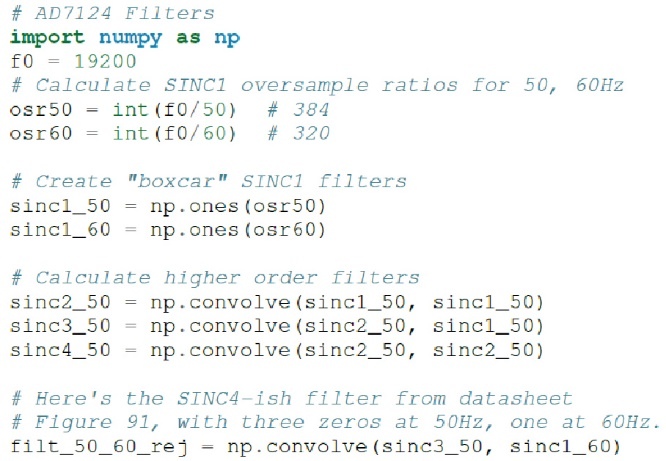
图13 适用于50Hz/60Hz sinc滤波器的AD7124-8代码示例

滤波器的脉冲（时域）形状如图14所示。滤波器系数(tap)值被标准化，以得出零频率时的单位(0dB)增益。

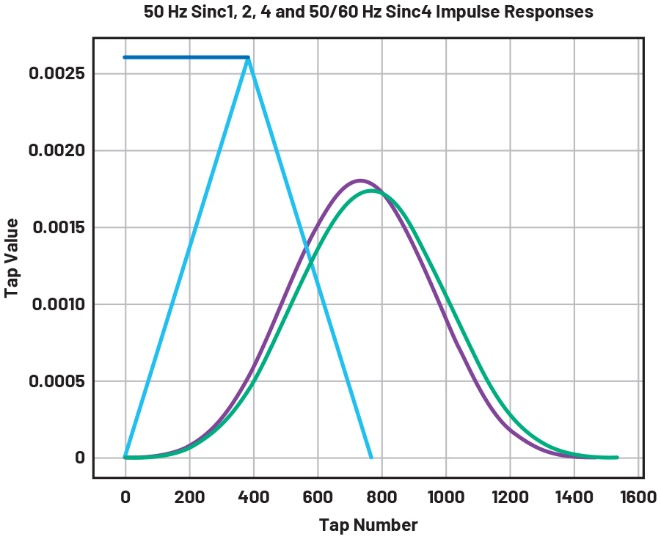
图14 对矩形脉冲响应进行反复卷积，得到三角形响应，然后是类高斯脉冲响应

最后，可以使用NumPy的freqz函数计算频率响应，如图16所示。响应如图15所示。

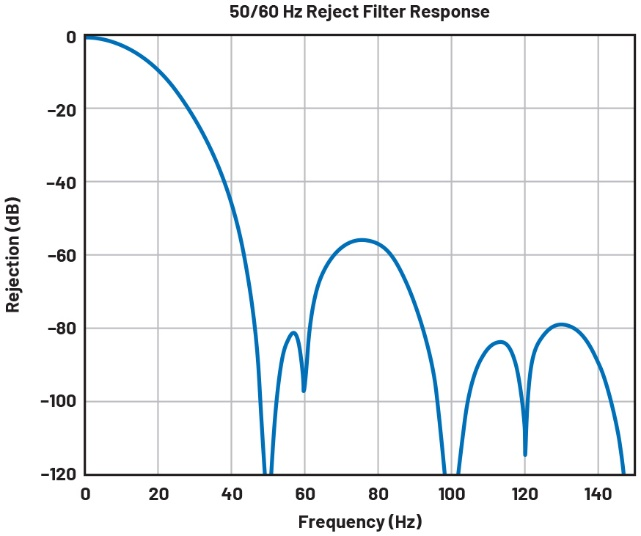
图15 将sinc3 50Hz陷波滤波器与sinc1 60Hz滤波器进行卷积，将产生强烈抑制50Hz和60Hz的复合响应

图16 AD7124-8代码示例，适用于带sinc 60Hz滤波器的sinc3 50Hz陷波滤波器

无可避免：传感器的基本限制

所有传感器，无论多么完美，都有最大输入值（和对应的最大输出，可能是电压、电流、电阻，甚至是刻度位置）和一个有限的本底噪声——即使输入完全静止，输出也存在“波动”。在有些情况下，提供电力输出的传感器可能包含具有有限电阻（更广泛一点，阻抗）的元件，在图17中，RSENSOR表示该电阻。这代表一个无法改善的基本噪声限值，此电阻会生成en(RMS)噪声电压，最小值为：

其中：eN (RMS)表示总噪声。K表示波尔兹曼常数(1.38e-23 J/K)。T表示电阻的绝对温度（开氏度）。F2和F1表示相关频段的上限和下限。将带宽标准化至1Hz，以V/√Hz为单位表示噪声密度。

传感器数据手册可能给出低输出电阻（通常接近0Ω），但这可能是个缓冲级，可以简化与下游电路之间的连接，但无法消除信号链前面部分的电阻导致的噪声。

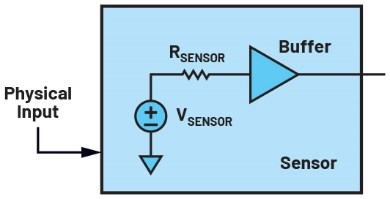
图17 传感器通常包括一个内部缓冲器，用于简化与下游电路的连接。当输出阻抗很低（通常接近0 Ω）时，来自高阻抗检测元件的噪声与信号一起被缓冲

还有许多其他的传感器限制——机械的、化学的、光学的，每个传感器都有自己的理论限制，我们可以模拟其影响，之后再进行补偿。但噪声是唯一无法弥补的缺陷。