基于BSM1的硝态氮浓度辨识建模
俞方罡,秦 斌(湖南工业大学,湖南 株洲 412000)
摘 要:污水处理过程复杂多样,为方便研究工作,根据基准仿真1号模型(Benchmark Simulation Modelno.1,BSM1)搭建simulink仿真模型。由于控制溶解氧和硝态氮浓度的稳定是污水处理过程的关键,所以针对传统PI控制对大滞后非线性系统中硝态氮浓度控制性能低以及系统运行速度慢的问题,利用极限学习机(ELM)和支持向量机(SVM)的预测能力对硝态氮浓度进行模型辨识和比较。结果证明,在数据量较少的情况下,支持向量机(SVM)具有很高的精确度,但是在数据量较高的情况下,极限学习机同样具有高精确度的特点并且运行速度更快。
关键词:污水处理;极限学习机;支持向量机;MATLAB仿真
0 引言
在污水处理中,活性污泥是应用最为广泛的处理方法,因此大量的研究工作都将活性污泥作为研究的对象。因为微生物存在的各种习性以及相互之间的作用,在最初的研究工作中学者们所提出的数学模型都存在结构非常复杂或是其应用受到限制的问题[1]。为了解决这些模型存在的问题,国际水协会(IWA)和欧盟科学技术合作组织(COST)两个组织合力开发的基准仿真1号模型[2]。为方便研究控制策略对污水处理过程的影响,对该模型进行了simulink建模及仿真[3-6],虽然通过简单的PI控制策略对此模型进行闭环仿真,但在系统为大滞后非线性的情况下,硝态氮浓度的控制效果并不理想[7-8]。随着人工智能和机器学习的不断发展,黄广斌提出了极限学习机,这是一种基于单隐层前馈型神经网络发展而来的智能算法,用于解决反向传播算法学习效率低、参数设定繁琐的问题[9-14]。宋剑杰、徐丽莎等人利用支持向量机解决出水COD、BOD的预测模型问题。对此,参考神经网络对非线性系统辨识能力强、具有强大的自学习能力的特点,在小数据组和大数据组两种情况下,采用极限学习机和支持向量机对硝态氮浓度进行模型辨识和比较[15]。
1 BSM1仿真及PI控制
基准仿真1号模型由ASM1活性污泥模型与Takács双指数沉淀模型组成。两种模型的搭建都遵守物料守恒定律,ASM1详细的描述了污水中组分的来源、反应过程和去向,用于搭建整个系统中生化池的部分。值得注意的是缺氧池1的入水由三方面组成;三个好氧池从外界受氧。因此此二者的物料守恒有别于上述规则,分别为式(1)与式(2)所示:
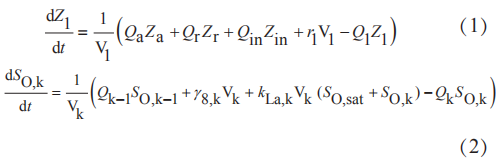
式中 Q 表示对应的流量,Z表示对应的组分,V表示对应生化池的容积,r为反应速率。但是ASM1并不能描述沉淀池的运行机理,由于BSM1中只需要考虑一维空间固相与液相的变化,因沉淀池的运行机理采用Takács双指数沉淀模型进行描述。如式(3)所示,式 中 Xf 为组分中易沉降颗粒性物质, Vs 为沉降速率,其余动力学参数均可查询得到。
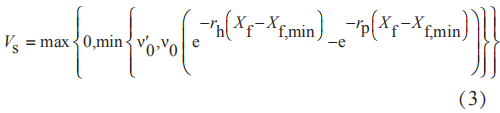
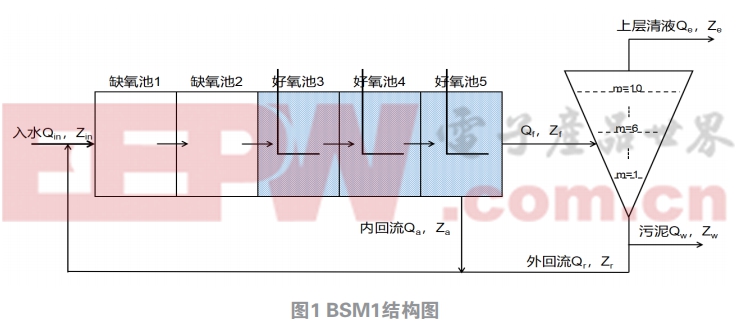
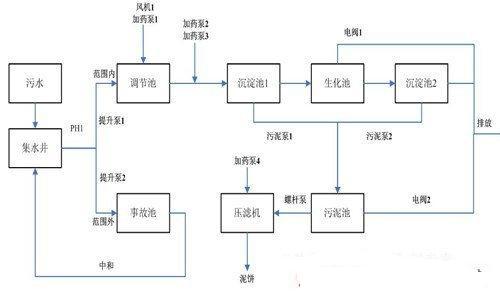
图1为BSM1结构图,箭头表示污水处理过程中水流方向,按A2/O工艺流程,前两个缺氧池容积均为1000 m3,后面三个好氧池容积均为1333 m3,最后沉淀池容积设定为6000 m3,根据ASM1与Takács模型可以在simulink中搭建模型如图2所示。可以看出基本与BSM1结构图是相同的,但是因为生化池的入水与出水有两种回流液的参与,所以需要加设水流混合模块与水流分离模块。由于污水处理模型方程复杂,为保证simulink的运行效率,生化池与沉淀池两个部分均采用S函数描述其内部机理。模型中所涉及的参数均查询得到。
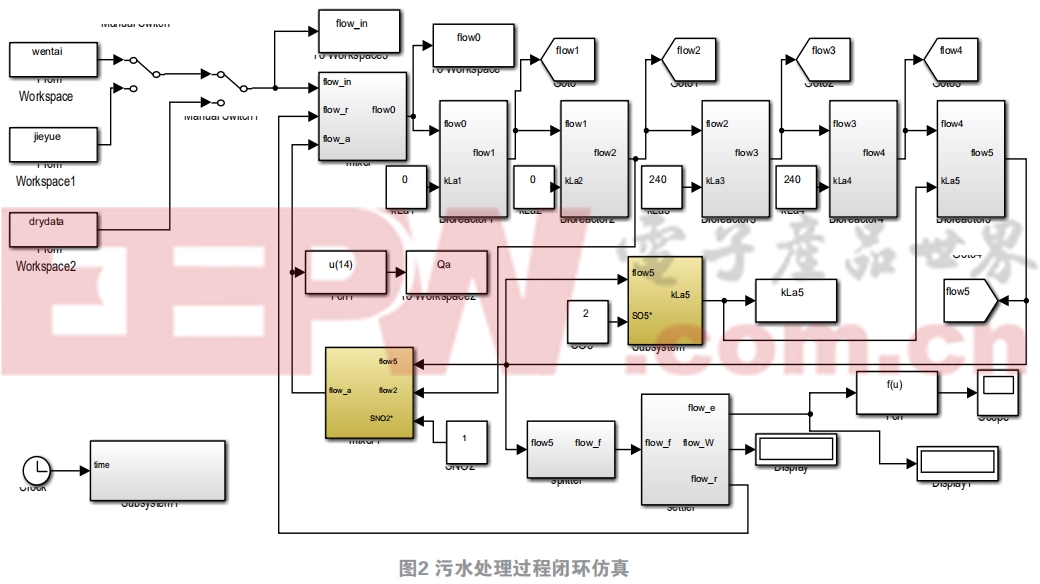
在此模型基础上,利用传统PI控制对模型进行闭环仿真。本文用三种不同的入水数据,即稳态入水数据、阶跃入水数据和实际入水数据,选择溶氧浓度和硝态氮浓度作为PI控制对 象 。 实际溶氧浓度一般在0.3 g/m3~7.45 g/m3之间,如此巨大的浓度波动是由于好氧池中的耗氧量在时刻变化而氧传递系数不变导致的,因此通过COD(COD能间接反映出池中耗氧量大小)的变化随时调整氧转移系数kla5来稳定溶氧浓度。同时好氧池溶解氧的浓度会影响缺氧池硝态氮浓度,在PI控制前,溶氧浓度在三种入水数据输入的情况下,输出曲线如图3所示。显然随着耗氧量的增加,溶氧浓度在随之减小。此时的氧传递系数是保持不变的,除稳态输入外,其他入水情况均使溶氧浓度和硝态氮浓度出现较大波动,虽然稳态入水能使溶氧保持稳定,但是浓度却没有达到要求。图4是硝态氮浓度的变化曲线,与溶解氧浓度相同,其波动范围非常大。
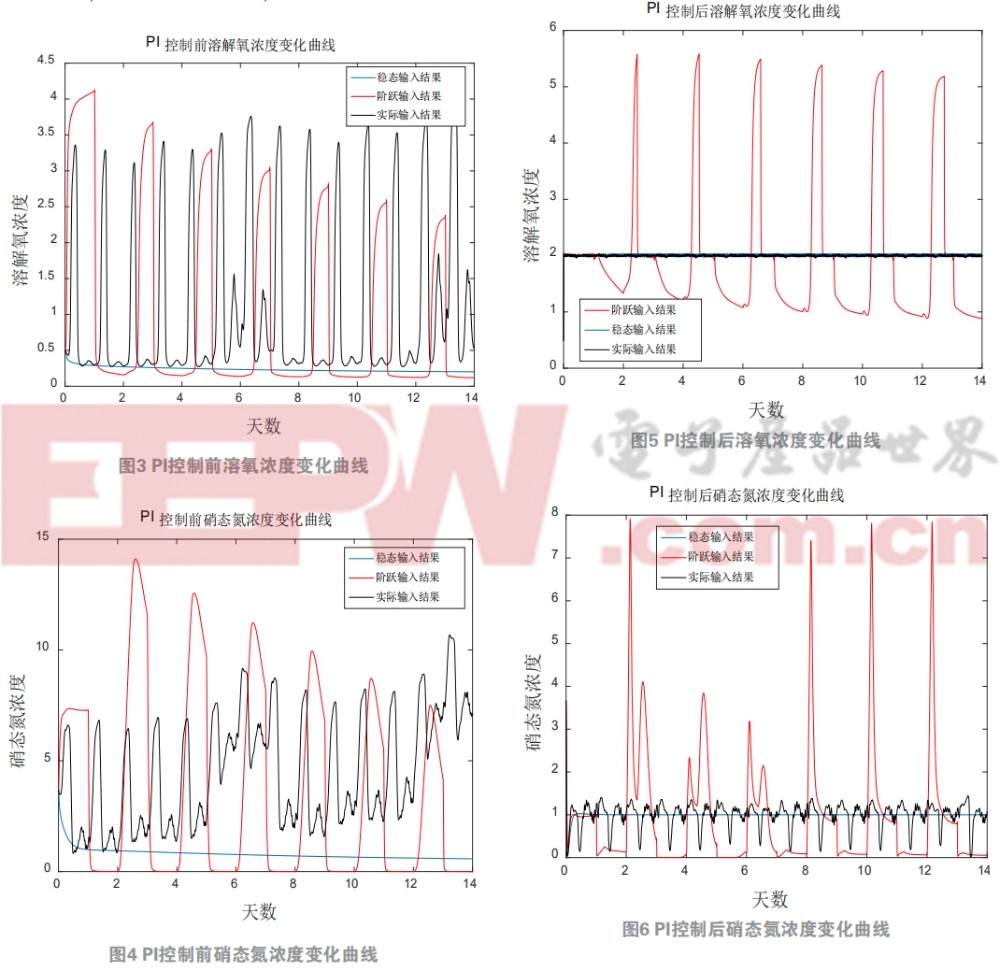
在图2位置加入PI控制器后,仿真的结果如图5和图6所示。阶跃输入情况下数据每次阶跃变化的幅度都很大,因此阶跃输入可以理解为多条稳态输入数据的集合,在每一次变化时相当于系统重新进行调节,存在一定的超调量但能迅速返回设定值,在实际输入情况下,溶氧浓度能够控制在了2 g/m3左右。但是缺氧池出水的硝态氮浓度波动范围依然较大,还有很大的优化空间。
2 模型辨识与结果对比
基准仿真1号模型中PI控制效果不够强大并且运行效率低下,主要原因在于BSM1参数多,模型复杂,工业生产中神经网络控制策略已经发挥了巨大作用,其对非线性系统的学习能力可以应用于污水处理过程控制中去,因此利用极限学习机和支持向量机建立污水处理中硝态氮浓度的简化模型。
南洋理工大学黄广斌教授提出极限学习机算法是由基于单隐层前馈型神经网络发展而来的智能算法,相比于前馈神经网络反向传播算法学习效率低、参数设定繁琐的问题,ELM避免了局部最优解的同时大大提高了学习速度,这在污水处理过程控制中非常重要。因为由单隐层前馈神经网络发展而来,其结构相同可表示为式(4)
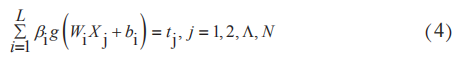
式中g(x)为激活函数;W为输入层到隐含层的权值;β为隐含层到输出层的权值;b为隐含层节点偏置。
这里采用sigmoid函数作为激活函数,以真实干燥天气入水数据作为采样数据,利用BSM1仿真模型采集2号缺氧池出水13个组分作为极限学习机的输入变量X,5号好氧池溶解氧浓度作为极限学习机的输出变量t,分别采集1345组作为小数据组和10000组作为大数据组,其中70%作为训练数据,30%作为测试数据,分别用训练数据和测试数据与实际数据进行对比。用矩阵可表示为式(5)

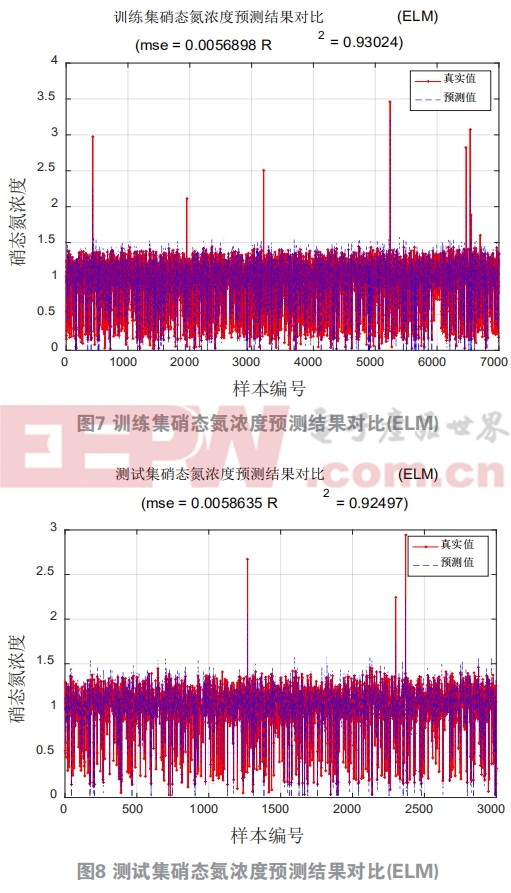
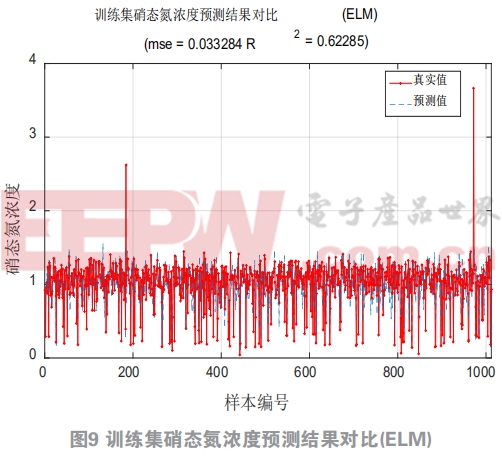
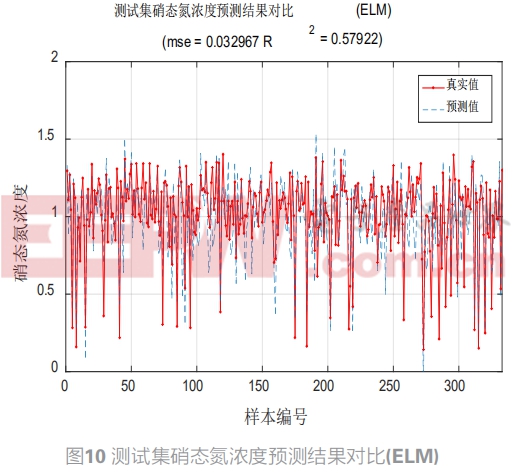
多数情况下H是不可逆矩阵,只有通过使代价函数最小化来寻找权值,由于极限学习机算法中随机给定初始输入权重W和节点偏置b,所以极限学习机的泛化性可以通过调节隐含层节点数L提高,同时理论指出单隐层神经网络权重幅值越小,网络的泛化性能就越强。这里选取节点数为300。图7图8为大数据组结果,图9图10为小数据组结果,在小数据组中,极限学习机的辨识精确度较低,但是在大数据组中极限学习机的运行速度依然很快并且具有较好的预测效果,训练集和测试集的性能指标都达到了0.9以上。
为比较极限学习机污水处理预测模型的预测性能,建立支持向量机污水处理预测模型,支持向量机相比于普通的神经网络,在学习复杂的非线性方程时能够提供一种更清晰更强大的方式。由于污水处理系统非线性程度很高,样本数量与特征量数量差距非常大,容易出现欠拟合和过拟合的问题,为了使SVM具有良好的泛化性,需要在代价函数中加入正则化风险,代价函数如式(6)所示:

式中ei为i号样本的误差; 1/2ωTω为正则化风险,用真实干燥天气入水数据作为采样数据,对作为输入变量的5号好氧池出水13个组分和作为输出变量的硝态氮进行采集,同样采样1345组数据作为小数据组和10000组作为大数据组,其中70%作为训练数据,30%作为测试数据,分别用训练数据和测试数据与实际数据进行对比。图11图12为大数据组结果,图13图14为小数据组结果,小数据组中,无论是训练集还是测试集,支持向量机的辨识精度远高于同组的极限学习机,图中红色实线的真实值和蓝色虚线的预测值基本保持一致,支持向量机对于内回流中的硝态氮浓度有很好的预测效果。但是在大数据组中,支持向量机的精度优势已经不再具备,相反其运行速度却远低于极限学习机。

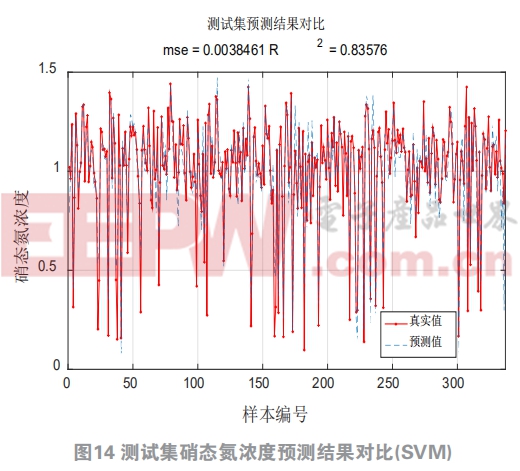
极限学习机的训练速度远高于支持向量机,因为极限学习机算法中直接生成初始化输入权重和隐含层节点偏置,不需要迭代调整,而支持向量机对正则化参数和核函数参数的选取比较费时,极限学习机通过调整隐含层节点数可以调节模型的泛化性和预测精度,相比于支持向量机运用更加简便。在数据量比较少的情况下,支持向量机的辨识精度很高,具有明显的优势,但是数据量较多的时候,极限学习机的精度不比支持向量机低,同时拥有更快的辨识速度,此时极限学习机要优于支持向量机。
3 结论
污水处理过程是个长时间过程,对处理系统进行基于BSM1的simulink建模提高了研究工作的效率,针对PI控制对硝态氮浓度控制能力低下的问题,建立基于ELM的简化模型和基于SVM的简化模型。结果表明,两者都有不错的大滞后非线性系统的模型辨识性能,SVM的辨识精度很高,但在数据量很大的情况下,ELM的精度也同样很高,其建模简单,训练速度快的特点更具优势。现在污水处理过程中对数据进行采集是普遍的现象,这些数据对神经网络来说是非常重要的部分,具有不同针对性的污水处理过程是可以采用不同的神经网络建模,无论是ELM还是SVM都为污水处理提供了非常有效的方法,溶解氧浓度和硝态氮浓度稳定是污水处理过程控制的关键,精确的预测模型对提高控制性能有重要作用。
参考文献
[1] 李春阳. 基于ASM1活性污泥污水处理过程的建模与控制问题研究[D].哈尔滨:哈尔滨工业大学,2016.
[2] 王藩, 王小艺, 魏伟,等. 基于BSM1的城市污水处理优化控制方案研究[J]. 控制工程, 2015, 22(6):1224-1229.
[3] 张琪. 活性污泥法城市污水处理系统的建模与仿真[D]. 北京:北京化工大学, 2015.
[4] Gaitang H , Junfei Q , Honggui H . Wastewater treatmentcontrol method based on recurrent fuzzy neural network[J].Ciesc Journal, 2016.
[5] 乔兴宏. 污水生化处理系统的智能预测及鲁棒优化控制研究[D].广州:华南理工大学,2016.
[6] 周红桃. 焦化污泥热解资源化与废水处理能量当量建模及节能优化[D].广州:华南理工大学.
[7] 王雨萌. 基于智能控制策略的污水处理控制系统[D]. 杭州:浙江大学,2018.
[8] 刘帮, 秦斌, 彭小玉. 污水出水水质的SVR建模[J]. 新型工业化,2015(1).
[9] 许玉格, 邓文凯, 邓晓燕, et al. 基于核函数的加权极限学习机污水处理在线故障诊断方法[J]. 化工学报.
[10]宋翼颉, 王欣. 基于LSSVM的污水处理过程预测控制[J]. 新型工业化, 2015(8):33-38.
[11]林梅金. 污水生化处理系统的智能预测及优化控制策略研究[D].广州:华南理工大学,2015.
[12]王欣, 宋翼颉, 秦斌,等. 基于LSSVM的污水处理过程建模[J]. 湖南工业大学学报, 2016, 30(1):59-63.
[13]甘露. 极限学习机的研究与应用[D]. 西安:西安电子科技大学,2014.
[14]杨易旻. 基于极限学习的系统辨识方法及应用研究[D]. 长沙:湖南大学, 2013.
[15]秦斌, 易怀洋, 王欣. 基于极限学习机的风电机组叶根载荷辨识建模[J]. 振动与冲击, 2018.
本文来源于科技期刊必威娱乐平台 2020年第02期第49页,欢迎您写论文时引用,并注明出处。






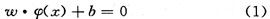
评论